Algorithm | Hirschberg's Algorithm

Notes: Hirschberg’s Algorithm, A Linear Space Algorithm for Computing Maximal Common Subsequences.

Hirschberg’s Algorithm 是一種用來解決 Needleman-Wunsch Algorithm 的空間複雜度的演算法，原本的空間複雜度為 O(m*n)。 在論文的發表時間(1975)，記憶體是一個很昂貴的資源，所以 Hirschberg’s Algorithm 的提出是一個很大的突破。

這個問題如果想要實際寫程式的話，可以參考 LeetCode 72. Edit Distance。

簡單的 Golang 實作，Golang Implementation.

Introduction

Edit distance

Edit distance 是針對兩個 String 之間的差異度的量化測量，可以用來判斷兩個字串之間的相似度，在 DNA 或 Unix 的 diff 等等應用上都有很大的用途。

Levenshtein distance 是指將一個字串變成另一個字串所需要的最少操作次數，操作包括 Insert, Delete, Replace。

• “Benson”, “Ben” 這兩個字串的 Edit distance 為 3
  • 要把 “Benson” 變成 “Ben” 需要做 3 次 Delete 操作
  • 要把 “Ben” 變成 “Benson” 需要做 3 次 Insert 操作

這邊會介紹 Needleman-Wunsch Algorithm 和 Hirschberg’s Algorithm 這兩個演算法，用來計算兩個字串之間的 Edit distance。

Needleman-Wunsch Algorithm

Needleman-Wunsch Algorithm, A general method applicable to the search for similarities in the amino acid sequence of two proteins.

Needleman-Wunsch Algorithm 是生物資訊中用來比對蛋白質或 DNA 序列的演算法，最早於 1970 年提出。是很標準的 Dynamic Programming 演算法，用來計算兩個序列之間的最佳對齊。

• Time Complexity O(mn), Space Complexity O(mn)

假如我們有兩個字串 Benson 和 Ben

Step 1: Create a DP Table

跟大部分的 DP 演算法一樣，我們需要先建立一個 DP Table，用來存放每個子問題的解，大小為 (m+1) * (n+1)。

Step 2: Choose a scoring system

假如兩個字串要做 Align 的話，每個位置只有三種可能的情況 match, mismatch, gap，在 Needleman-Wunsch Algorithm 中有很多種評分標準， 這裡使用 min 來作為評分方法的話，可以設計以下的 Scoring System:

• Match: 0
• Mismatch: 1
• Gap: 1

Step 3: Initialize the DP Table

現在我們依照 Gap 的評分標準，初始化 DP Table 的第一列和第一行。

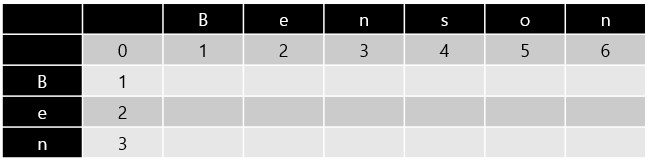
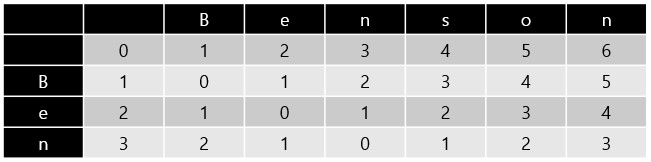
Step 4: Fill in the DP Table

• Dynamic programming recursive formula:

• 依照上面的 Recursive Formula 依序歷遍整個 DP Table，注意是以 Row-Major 的方式填入 DP Table
  • 如果 x(i) = y(j)，則 dp(i, j) 直接取左上角的值
  • 否則取 Left, Top, Left-Top + 1 的最小值

Step 5: Traceback

最後我們可以從右下角的位置開始往左上角回溯，因為之前使用的 Scoring System，這裡我們使用 Min trace back:

• ⇦ 代表左側的字串要塞入一個 Gap
• ⇧ 代表上方的字串要塞入一個 Gap
• ⇖ 代表這兩個字元是 Match

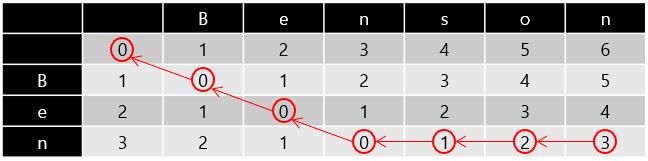
最後的 Alignment 結果如下，Benson 和 Ben 之間的 Edit distance 為 3:

Benson
Ben---

Prefixes Alignment

我們也可以發現在 DP Table 中，每個格子都代表該左側和上方的 Prefix 之間的 Edit distance，例如以下:

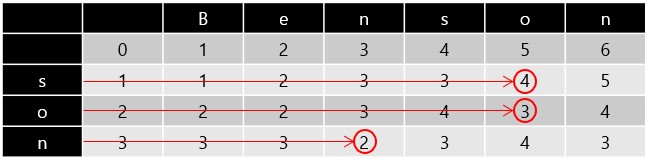
• ”s”, “Benso”, Edit distance is 4
• “so”, “Benso”, Edit distance is 3
• “son”, “Ben”, Edit distance is 2

但是在 DNA 比對中往往資料量很大，所以 Needleman-Wunsch Algorithm 的空間複雜度是 O(mn)，這樣的空間複雜度在當時的記憶體是一個很大的負擔。

Hirschberg’s Algorithm

Hirschberg’s Algorithm 可以在 Space Complexity O(min(m, n)) 的情況下，計算出 Needleman-Wunsch Algorithm 的結果， 並且保持 Time Complexity O(mn)，並且 Hirschberg’s Algorithm 是一個 Divide and Conquer 的演算法。

Divide and Conquer

首先要能做到 Divide and Conquer，我們需要確定一個 Base Case 被拆分後還是可以滿足原本的問題，所以為什麼可以進行拆分就會是接下來的問題。

• 假如有兩個字串 L, R 之間的 Edit-Distance 是 4
  • Len(L) = 8, Len(R) = 8
  • 代表要講 R 修改成 L 需要經歷至少 4 次的操作
• 假如我們可以做拆分的話，現在變成四段的字串如下
  • L₁ = L[1:6], L₂ = L[7:8]
  • R₁ = R[1:4], R₂ = R[5:8]
• 這裡必須保證 ED(L1, R1) + ED(L2, R2) = ED(L, R) 是相同的，這樣問題就來到我們怎麼找到一個點劃分 R
  • R 無論如何都會以 Len(R) / 2 作為拆分點

L = “CDEFABGH”, R = “ABCDEFGH”，以此為例會得到以下的結果

注意下圖中 “ABCDEFGH” 無論如何都是以中點拆分

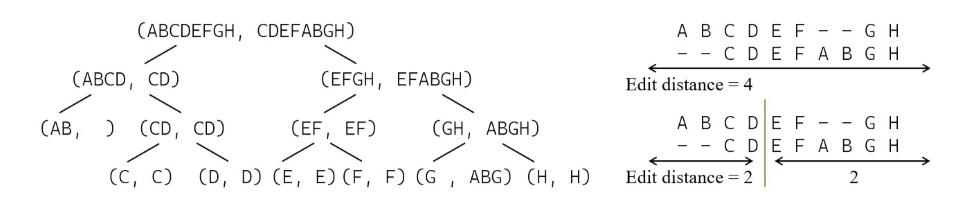
Needleman-Wunsch Algorithm

Needleman-Wunsch Algorithm 可以幫助我們找到適合拆分的位置，既然我們知道 R 必須被拆分，那我們就可以用 R₁ 和 R₂ 來計算出 L 適合的拆分點。

• 這裡使用的評分方式跟之前一樣，Match: 0, Mismatch: 1, Gap: 1

1. 將 L 與 R₁ 進行 Needleman-Wunsch Algorithm，得到 DP Table
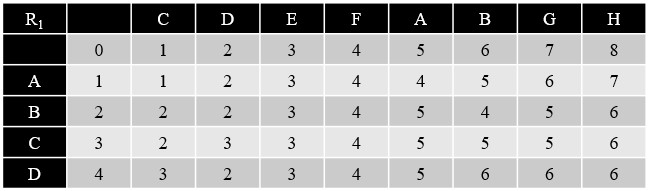
2. 將 Rev(L) 與 Rev(R₂) 進行 Needleman-Wunsch Algorithm，得到 DP Table
   • 因為我們要計算從後面往前的 Prefix 的 Edit distance，所以這邊要將字串反轉

   

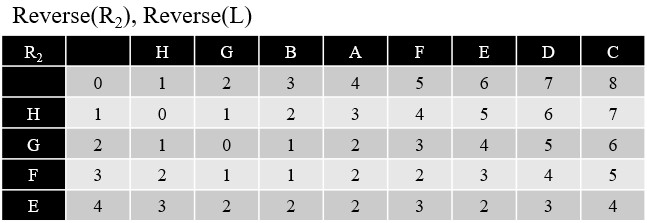
3. 分別將兩張 DP Table 組合會得到以下的結果
   • “ABCD” 到 “CDEFABGH” 的最小編輯距離在 “ABCD”, “CD”
   • “HGFE” 到 “HGBAFEDC” 的最小編輯距離在 “HGFE”, “HGBAFE”
   • 會發現其實就是取 R₁, L 和 Rev(R₂) 與 Rev(L) 的最小編輯距離，以這個點來分割 L 不會造成任何額外的編輯距離

   

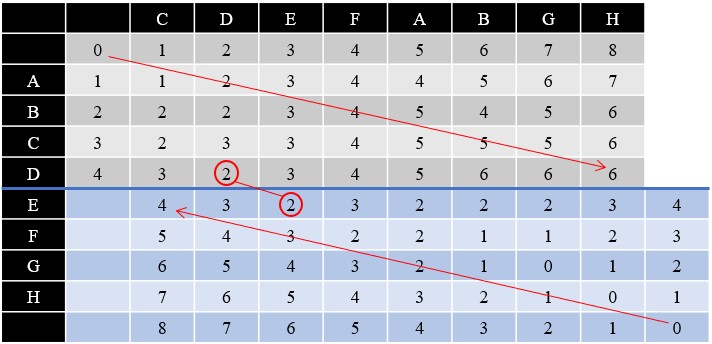
以上的方式就是使用 Needleman-Wunsch Algorithm 來找到適合拆分的點，在這裡我們做些總結

1. 將 R 使用 Len(R)/2 分為 R₁ 和 R₂
2. 使用 Needleman-Wunsch Algorithm 找到 R₁ 和 L 的最小 Prefix 編輯距離
3. 使用 Needleman-Wunsch Algorithm 找到 Rev(R₂) 和 Rev(L) 的最小 Prefix 編輯距離
   • Rev 的目的是從後面往前找到 Prefix 的編輯距離
4. 將兩個 DP Table 的最後一列相加，找到各自對 L, Rev(L) 的最小 Prefix 編輯距離，即是 L 的拆分點

時間複雜度不會改變是 O(mn)，但是空間複雜度可以降到 O(mn)，因為需要一個剛好 mn 的 DP Table。

Optimize Space Complexity

在這裡我們能發現在 Needleman-Wunsch Algorithm 中，我們其實只需要保留兩列的 DP Table(各自的最後一列)， 因此在 DP Table 的建立過程中並不需要把整個表的空間都保留下來，只需要一個上方列的 1D Array 就可以建立 DP Table。

• 這樣的空間複雜度就可以降到 O(min(m, n))
• 在 Divide and Conquer 的第一步我們可以先選擇較小的字串作為 R，這樣可以減少空間的使用

Last Edit

06-04-2024 00:43