Note | Gomoku AI - Game Tree
練習基礎AI演算法的入門題目,博弈樹搜尋與啟發式演算法,順手完成一個 GUI 小遊戲。
Introduction
傳統的AI演算法題目,以非神經網路的方式來嘗試AI撰寫。睡不著乾脆更新下Blog,至少忙起來能讓我轉移一些注意力,順便做個筆記。
博弈樹(Game Tree)其實就是一種將賽局中所有可能展開後的 Tree,那其中的每個 Node 就代表著遊戲進行中的某個狀態, 那我們以 Tic-Tac-Toe (井字棋)來看,就會有 26830 種遊戲過程。
Tic-Tac-Toe 的棋盤大小不過才 3x3 就有 26830 種可能,那五子棋的棋盤為 15x15 一個簡易的算法是 15! 幾近是天文數字。 如果想以全部遍歷的方式來找出最佳解幾乎是不可能做到的事,那這時就需要一些策略去找出最佳路徑,所以我們會用到幾種算法。

- Maximin algorithm. (對抗性的搜尋算法)
- Alpha Beta pruning. (剪枝算法)
- Heuristic. (啟發式算法)
Maximin algorithm
Maximin algorithm (極大極小值演算法),是一種找出失敗的最大可能性下的最小值的演算法,這是 wikipedia 上的解釋。 簡單來說在一個五子棋博弈樹中,必然有兩個不同的玩家互相下棋,故博弈樹我們也可以分成玩家層與AI層來看待,因此在搜尋的過程中我們要去找尋每一層的最有利狀態, 最後去找到玩家下的最好的狀態下,AI能下出的最佳步驟。
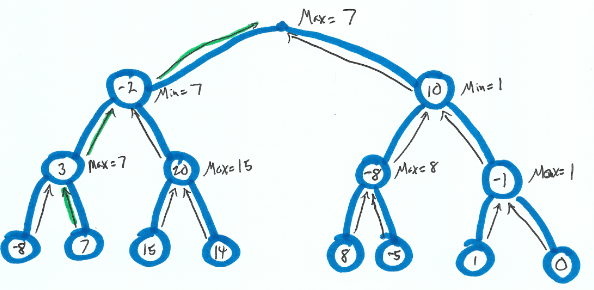
其實看上圖就能發現其實就跟 Max-Min-Heap 很相像,只是今天 Heap 是從下往上, 但 Tree 是從上往下,一個中序遍歷的搜尋方式。在搜尋過程中我們要去找到都是極大或極小的路徑, 但是如果我們真的去遍歷整個棋盤,時間複雜度將為 O(b2), 在棋盤為15*15,深度為4的情況下,2254是一個非常慢的演算法。
Alpha Beta pruning
但是即便我們能做到棋盤的對抗搜尋,但是搜尋時間還是很慢,因此我們需要去做到剪枝的動作, 放棄不可能的分支做搜尋,把希望放在更有可能的分支上以做到更深的深度。在最糟的情況下, 時間複雜度將為 O(b2),而在最佳的情況下有機會達到 O(sqrt(bd)),
實作上我們就是在遞迴時,如果當前層數為極大層,但是下下層出現一個比最大值還要小的節點我們就直接剪掉, 因為我們要找的是極大值,就不用去考慮更小的值了,同理運用在極小層。

Wikipedia中圖的第三層中的 7 節點其實也是要剪掉的,圖有錯誤。
Heuristic
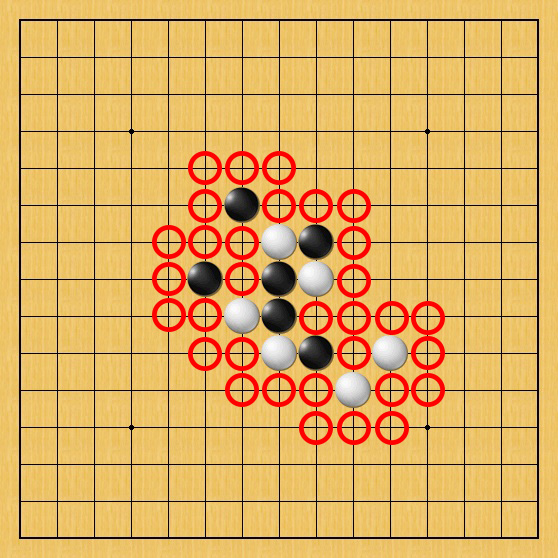
但是即使我們能做到剪枝搜索時間還是平均需要 O(b3d/4),但同時我們也知道初始的搜尋節點很重要, 如果一個棋盤如下圖,我們以一個2D Array來實現這個棋盤狀態,像是 x, y = 0, 0這樣的位置如果不會影響大局完全沒有搜尋的必要。
| State | Operate |
|---|---|
| 五子 | 直接返回 |
| 活四 | 直接返回 |
| 活三 | … |
| 死三 | … |
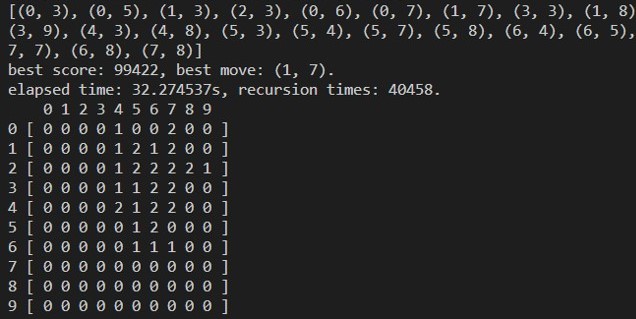
因此我們可以在尋找搜尋節點以有鄰居的空位為主,並且加入一些評分機制來對這些位置排序:
把每次搜尋的位置 print 出來來觀察搜尋的順序與影響。除去五子活四這種直接將軍的局面, 剩下的依照分數排序來做搜尋,這樣我們能更快的找到最佳的路徑, 分數不符的路徑就將會被剪掉,把時間用來做到更深的搜尋層數。
要記住即便使用了啟發式函數,但是只要局面變得複雜,搜尋速度同樣會下降很多, 畢竟每做一個搜尋就是需要付出 Pd 的時間消耗,因此排序並消除不重要位置的步驟就很重要。
Note
- 寫輔助函數時的注意事項
- 在寫這些輔助函數的時候,要盡量減少做整個棋盤的搜尋動作,同時可以嘗試將棋盤視為字串, 這樣就能以 Regex 來處理連線確認將會大幅加快執行速度,尤其是如果你的棋盤
- 評估函數要仔細設計
- 評估函數;尋找的棋形;搜尋深度;是最直接的影響棋力的選項,如果AI的落子有問題, 通常應該往這幾個方向做修改,例如搜尋深度與評估函數設計不好就有可能使AI自殺的情形發生。
NOTE
之後更新,目前已完成一個簡易的算法在Github,希望能在過年前把它做到一個更滿意的狀態。