September 21, 2023

Compiler | Lexical Analysis Notes

Compilers course notes from CCU, lecturer Nai-Wei Lin. Lexical analysis(語彙分析) 將文本轉換為有意義的語彙標記(Token)，這通常是 Compiler 步驟的第一步。

Compilers: Principles, Techniques, and Tools 介紹使用 Regular Expression(RE, 正規表達式)描述 Lexemes 的方法，並透過一個 Lexical-analyzer generator(語彙分析器生成工具)來進行代碼生成，使我們可以專注在如何描述 Lexemes。

因此會先學習 RE 的使用方法，RE 能被轉換為 Nondeterministic Finite Automata(NFA, 非確定有限狀態自動機)問題在轉換為 Deterministic Finite Automata(DFA, 確定有限狀態自動機)問題，之後就能用程式碼模擬自動機運作。

3.1 The Role of the Lexical Analyzer

Lexical analyzer(語彙分析器)主要任務就是讀取 Source code 的輸入字符(characters)，並將其組成為 Lexeme，並輸出一個 Token 序列，並在識別到 Identifier 時要將其添加到 Symbol table 中。

下圖顯示一個 Syntax analyzer(語法分析器)與 Lexical analyzer 互動的過程，呼叫 getNextToken 來使語彙分析器不斷讀取字符，直到識別出下一個 Token 將其返回給語法分析器。

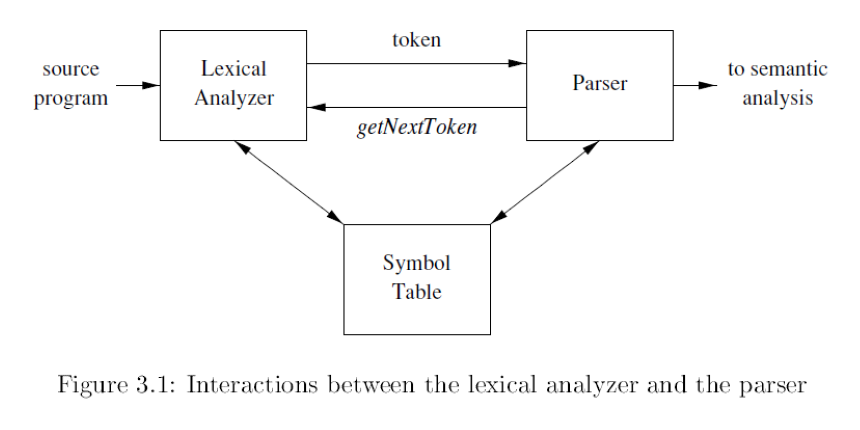
語彙分析器可以被劃分為兩個骨牌效應的過程:
- 掃描不需要轉變為 Token 的部分的過程
  - 例如: 過濾 Comments, Whitespace (blank, newline, tab …)
- 實際的 Lexical analysis，從掃描的輸入中產生 Token

語彙分析器還可以將 Compiler 的錯誤訊息與 Source code 的發生位置聯繫起來，例如:

紀錄換行符號的行數，以便在出錯時給予一個行數

某些編譯器中會將 Source code 複製一份，並將錯誤訊息插入該位置

3.1.1 Lexical Analysis Versus Parsing

把 Lexical analysis(Scanning) 與 Syntax analysis(Parsing) 分開有三個原因:

簡化編譯器設計，分離可以更好的專注在不同任務上
- 如果我們正在設計一種新的語言，將詞法和語法問題分開也可以使整體語言設計更加清晰
提高編譯器的效率
- Lexical analyzer 獨立後我們就可以去更方便的優化 I/O 的處理
提高編譯器的可移植性，輸入設備特定的特性可以限制在詞法分析器中
- 例如: Windows 的換行符是 \r\n，Linux 上的是 \n

延伸閱讀 Input Buffering in Compiler Design

3.1.2 Tokens, Patterns, and Lexemes

在討論 Lexical analyzer，這裡有三個需要了解的術語:

token(language): a set of strings
- if, identifier, relop
Pattern(grammar): a rule defining a token
- if: if
- identifier: letter followed by letters and digits
- relop: < or <= or = or <> or >= or >
Lexemes(sentence): a string matched by the parrern of a token
- if, Pi, count, <, <=

假設有以下 Clang code，依照 Figure 3.2 print 與 score 是 Token id 所匹配的 Lexeme，"Total = %d\n" 則是與 literal 匹配的 Lexeme。

printf("Total = %d\n", score);

在很多程式語言設計中，大部分 Token 被分成以下幾類:

Reserved words(保留字)都有一個 Token，保留字的 Pattern 與保留字相同
Operators 的 Token，可以表示單個運算符，也有像 comparison 有多個同類別的運算符
Identifier 只用一種 Token 表示
Constants 有一個或多個 Token，例如 number、literal
Punctuation symbol 都有各自的 Token，例如 (, ), ,, ;

3.1.3 Attributes for Tokens

Attributes 是用來區分 Token 中的不同 Lexeme，例如 0, 1 都能跟 Token number 匹配，因為 Lexcial analyzer 很多時候不能僅返回給 Syntax analyzer 一個 Token name， Token name 影響 Syntax analyzer，而 Attributes 會影響 Parsing 之後的 Semantic analyzer。

< if, >
< identifier, pointer to symbol table entry >
< relop, = >
< number, value >

3.3 Specification of Tokens

Token 的一種重要的表示方式(規格)就是 Regular expression，RE 可以高效的描述處理 Token 時要用到的 Pattern。

3.3.3 Regular Expression

Regular Expression(RE, 正規表達式)是由較小的 RE 按照以下規則遞迴建構，下面的規則定義了某個 Alphabet ∑ 的 RE:

ε 是一個 RE，L(ε) = {ε}，也就是該語言只包含空字串
如果 a 是 ∑ 中的符號，那麼 a 也是一個 RE 代表 L(a) = {a}，也就是說這個語言僅包含長度為 1 的字串 a。

Suppose r and s are RE denoting L(r) and L(s)
(r) (s) is a RE denoting L(r) ∪ L(s)
(r)(s) is a RE denoting L(r)L(s)
(r)* is a RE denoting (L(r))*
(r) is a RE denoting L(r)

Example:

a | b               {a, b}
(a | b)(a | b)      {aa, ab, ba, bb}
a*                  {ε, a, aa, aaa, ...}
(a | b)*            the set of all strings of a's and b's
a | a*b             the set containing the string a and all strings consisting of zero or more a's followed by a b

Order of operations:

Priority	Symbol
Highest	\
High	(), (?:), (?=), []
Middle	*, +, ?, {n}, {n,}, {n,m}
Low	^, $
Second lowest	concatenation
Lowest	\|

Algebraic laws:

3.3.4 Regular Definitions

為了方便表示，我們可能會給某些 RE 別名，並在之後的 RE 中使用符號一樣使用這些別名，例如:

Name for regular expression
$d_1 \rightarrow r_1$
$d_2 \rightarrow r_2$
$…$
$d_n \rightarrow r_n$
$where\;r_i\;over\;alphabet\cup ( d_1, d_2, …, d_{i-1} )$
Examples:
$letter \rightarrow A | B | … | Z | a | b | … | z$
$digit \rightarrow 0 | 1 | … | 9$
$identifier \rightarrow letter(letter | digit)*$

上面的 Examples 定義了一個僅能由 letter 開頭但的 identifier

3.3.5 Extensions of Regular Expressions

RE 後續有其他的擴展，用來增強 RE 表達字串的能力，這裡會介紹最常被使用的幾種擴展

One or more instances
(r)⁺ denoting (L(r))⁺
r* = r⁺ | ε
r⁺ = rr*
Zero or one instance
r? = r | ε
Character classes
[abc] = a | b | c
[a-z] = a | b | … | z
[^a-z] = any character except [a-z]
Examples:
$digit \rightarrow 0 | 1 | … | 9$
$digits \rightarrow digit^+$ $number \rightarrow digits(.digits)?(E[+-]?digits)?$

上面的 Examples 定義了從 digit 到 digits 最後到 number 的過程

3.6 Finite Automata

這裡 3.6/3.7 章不會依照課本順序，而是依照課程進度。
NFA 的 Transition function 可以指向多個 State，DFA 的 Transition function 只能指向一個 State
會先介紹相對簡單的 DFA 再介紹 NFA，這樣可以更容易理解 NFA 的運作

要注意自動機的幾個特性:

自動機是 Recongnizer(識別器)，他們只能對輸入的字串進行判斷 “Yes” or “No”
Finite automata 分為兩類
- Nondeterministic finite automata (NFA, 非確定有限狀態自動機)
  - A symbol can label several edges out of the same state, the empty string(ε) is a possible label.
- Deterministic finite automata (DFA, 確定有限狀態自動機)
  - For each state, and for each symbol of its input exactly one edge with that symbol leaving that state.

3.6.1 Nondeterministic Finite Automata

An NFA consists of:

A finite set of states
A finite set of input symbols, default empty string is not in the set.
A transition function (or transition table ) that maps (state, symbol) pairs to sets of states
A state distinguished as start state
A set of states distinguished as final states

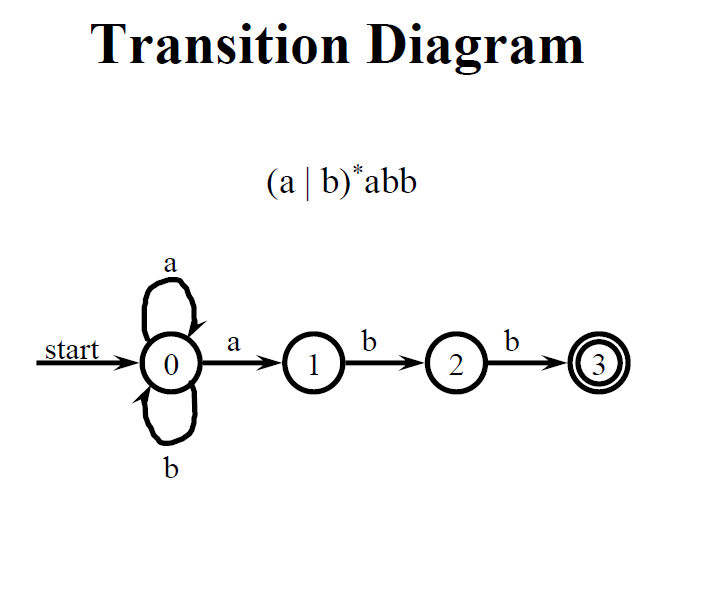
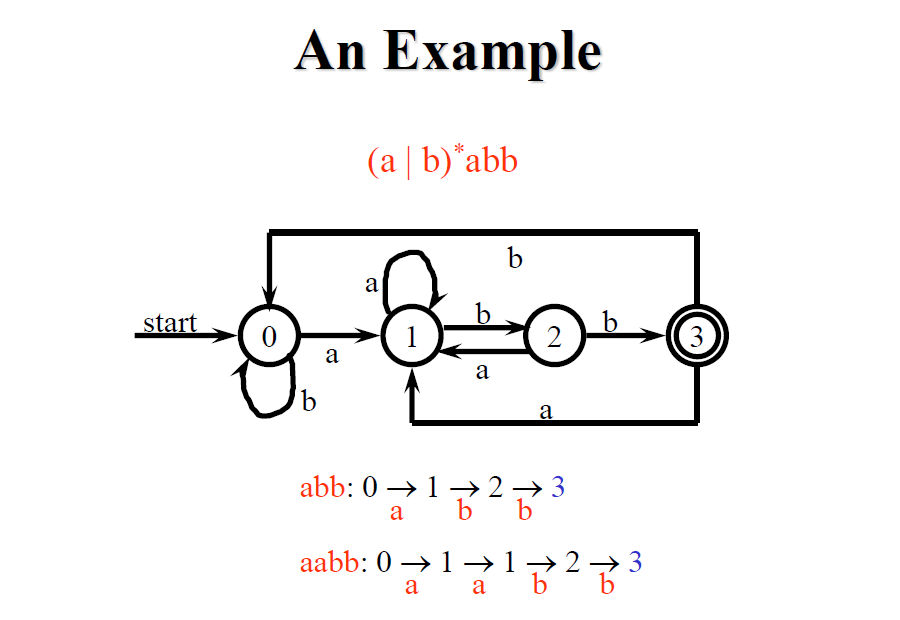
上圖左是 NFA’s transition graph 在狀態 0 有 a, b 兩種狀態轉移，圖右是他對應的範例

3.6.2 Transition Tables

NFA 可以表示為一張 Transition table(轉換表)，例如:

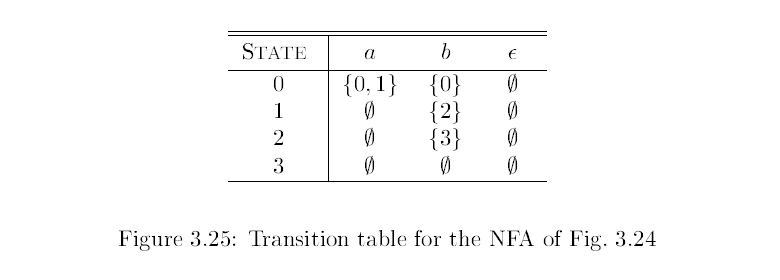
轉換表可以更容易看出 NFA 的狀態轉移，缺點是當 NFA 狀態(Alphabet)很多時，轉換表會變得很大佔用空間

3.6.3 Acceptance of Input Strings by Automata

NFA accept 輸入字串 s，如果從 Start state 開始，有一條路徑可以走到 Final state，這條路徑的轉移符合這個 Automata 所定義的語言

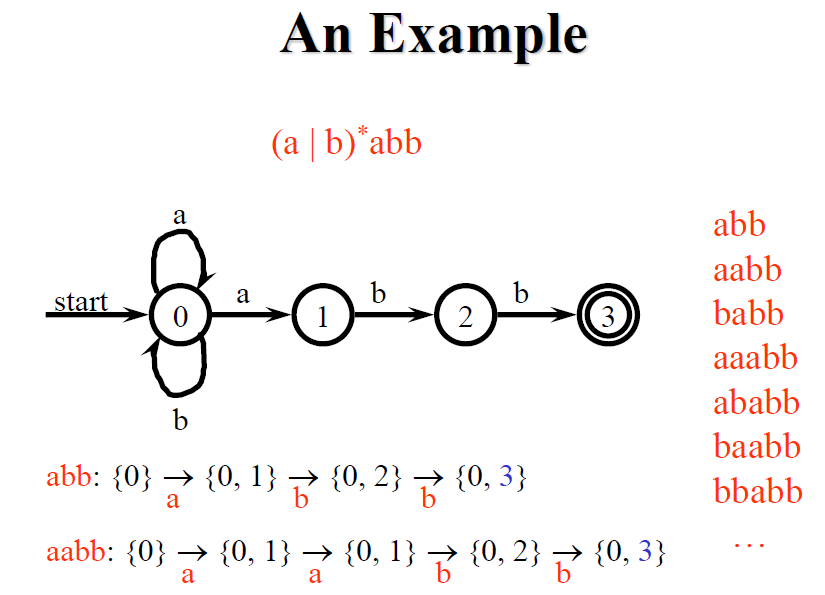
3.6.4 Deterministic Finite Automata

這裡會先談一個 DFA 怎麼用程式碼模擬，因為相較於 DFA 簡單許多

Deterministic finite automata (DFA, 確定有限狀態自動機) 是 NFA 中的一種特例，其中:
- There are no moves on input ε
- For each state s and input symbol a, there is exactly one edge out of s labeled a.
Algorithm 3.18 : Simulating a DFA. from Compiler: Principles, Techniques, and Tools p.150
- Input: An input string ended with eof and a DFA with start state s 0 and final states F.
- Output: The answer “yes” if accepts, “no” otherwise.

begin
s := s0;
c := nextchar;
    while (c != EOF) do begin
        s := move(s, c);
        c := nextchar;
    end;
    if (s ∈ F) then return "yes";
    else return "no";
end;

3.6.5 Simulation of an NFA

NFA 與 DFA 在模擬上的演算法幾乎一樣，最大的區別在於 ε-closure() 的建構，因為 NFA 在給定輸入的狀況下可以存在多個 State，因此在模擬上需要處理 State set。課本中會在 3.6.4 提前介紹 Algorithm 3.18 : Simulating a DFA. - p.151

Algorithm 3.22 : Simulating a NFA. from Compiler: Principles, Techniques, and Tools p.156
- Input: An input string ended with eof and an NFA with start state s 0 and final states F
- Output: The answer “yes” if accepts, “no” otherwise.

begin
S := ε-closure({S0});
c := nextchar();
    while (c != EOF) do begin
        S := ε-closure(move(S, c));
        c := nextchar();
    end;
    if (S ∩ F != ∅) then return "yes";
    else return "no";
end;

上面的 Pseudocode 模擬 NFA 的運作，其中:
- move(s, c): 從 state s 輸入 c 可以到達的 NFA state set
- move(S, c): 從 state s set S 輸入 c 可以到達的 NFA state set
- ε-closure(s): 沒有輸入字元，從 state s 僅通過 ε-transitions 可以到達的 NFA state set
- ε-closure(S): 沒有輸入字元，從 state s set S 僅通過 ε-transitions 可以到達的 NFA state set
- nextchar(): 回傳下一個輸入字元

注意上面的 S 是 NFA state set，而 s 是 NFA state

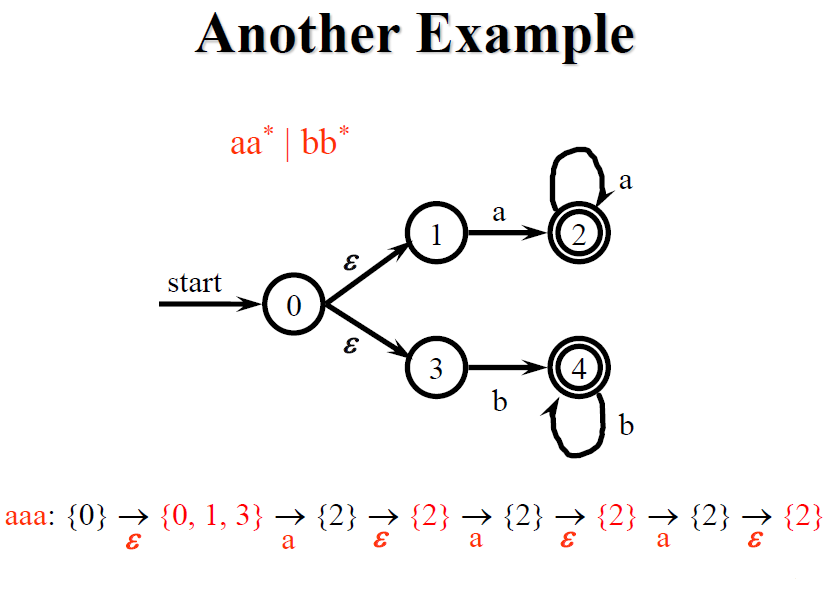
上圖左邊的最後的 S 與 Final state {3} 有交集，因此回傳 “yes”，右邊的則沒有交集，回傳 “no”

注意上圖的 NFA 並沒有加入 ε-closure() 因為沒有任何 ε State，因此可以只透過 move() 來模擬 NFA 運作

3.6.6 Computation of ε-closure

從上面的例子可以說明 move() 是如何運作，接下來這裡會講解 ε-closure() 是如何運作，用一個 DFS 來找出所有可以到達的 ε-State，返回一個 T set

Computing ε-closure(T)

Input: An NFA and a set of NFA states S.
Output: T = ε-closure(S).

begin 
    push all states in S onto stack;
    T := S;
    while stack is not empty do begin
        pop t, the top element, off stack;
        for each state u with an edge from t to u labeled ε do begin
            if u is not in T then begin
                add u to T;
                push u onto stack;
            end;
        end;
        return T;
end;

上面的例子看似複雜，其實只是組合了 move() 和 ε-closure() 的運作

3.7 From Regular Expressions to Automata

從 RE 轉換為 NFA，再從 NFA 轉換為 DFA，這裡會用這樣的順序來介紹

3.7.1 Construction of an NFA from a Regular Expression

使用 McNaughton-Yamada-Thompson construction algorithm，可以將 RE 轉換為 NFA。

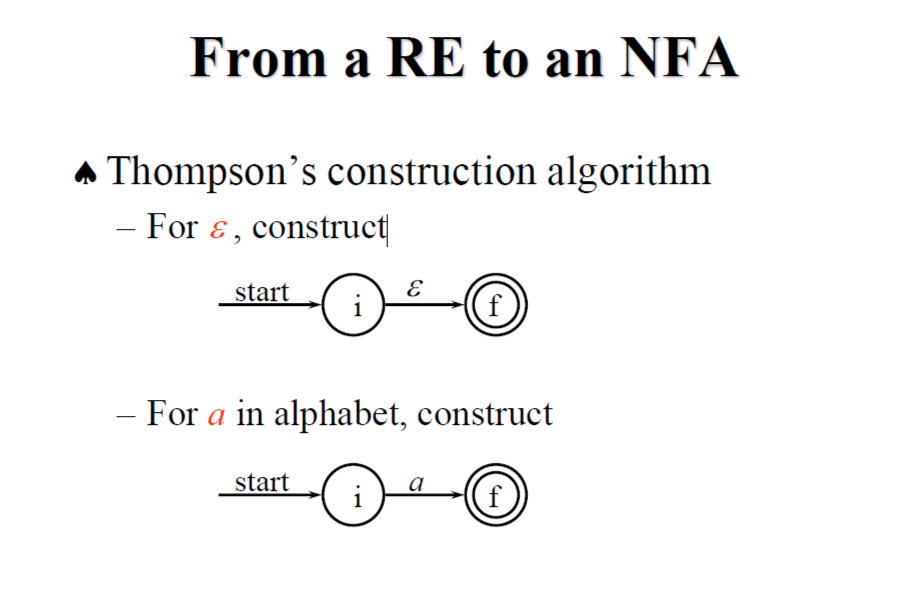
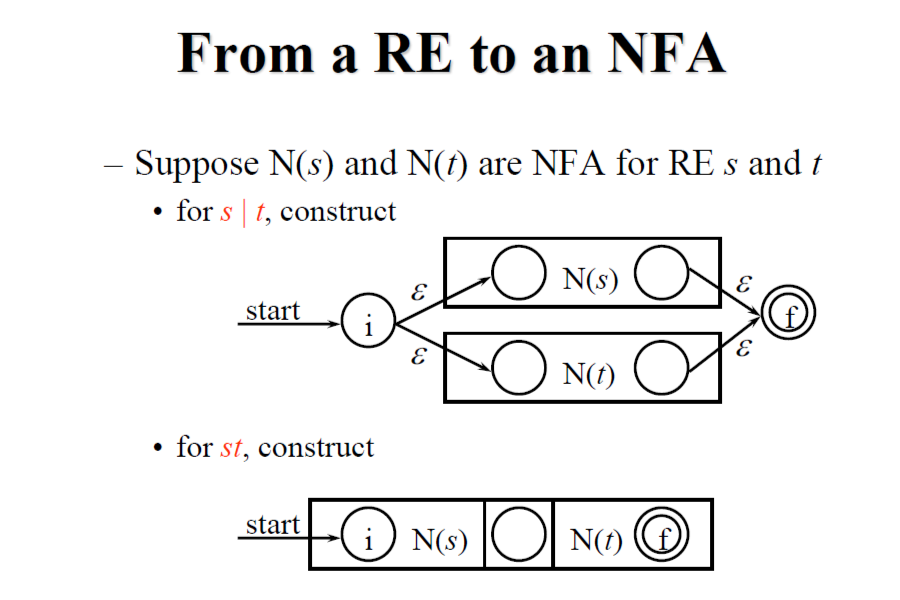
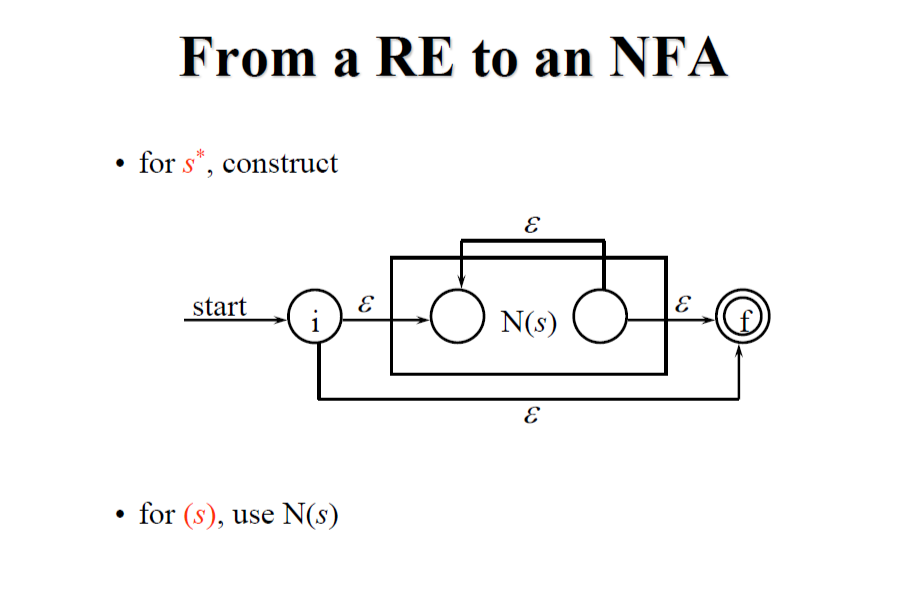
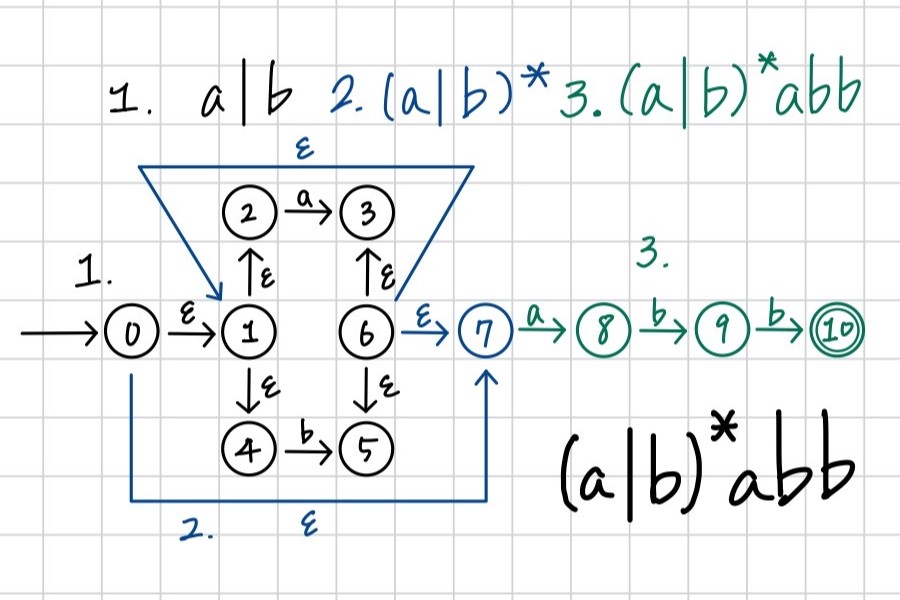
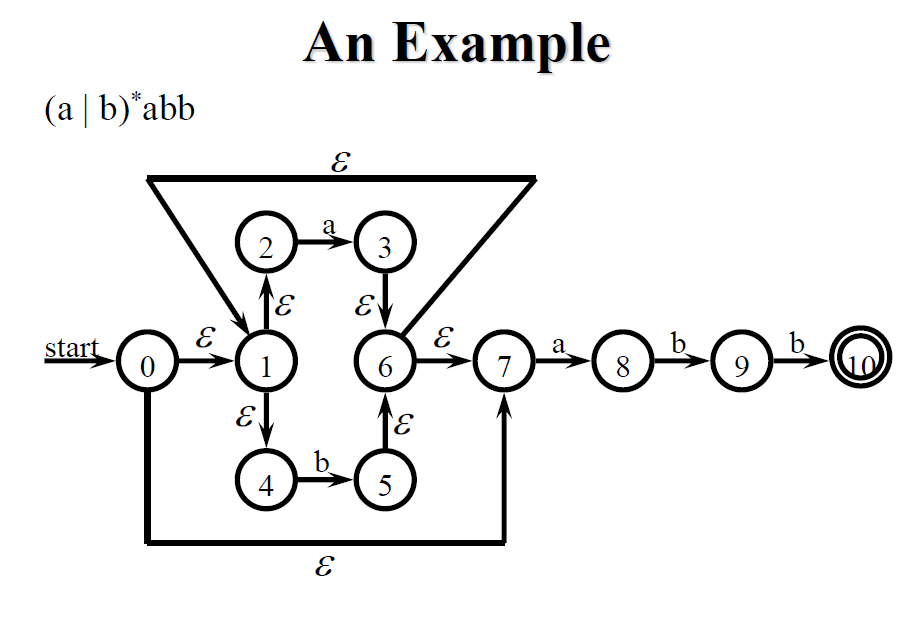
以上說明了 (ε), (a), (s|t), (st), (s), 的轉換過程，跟使用 (a|b)abb 作為例子來一步步轉換

在 Compilers: Principles, Techniques, and Tools p.161 - Example 3.24 有類似的轉換過程

3.7.2 Conversion of an NFA to a DFA

使用 Subset construction algorithm，可以將 NFA 轉換為 DFA。

Subset construction 的概念是 DFA 的每個 State 都對應 NFA 的一組 State，也就是 DFA 的每個 State 都代表 NFA 在讀取相同輸入後可能存在的所有狀態。但是這樣的話 DFA 的 State 數量會變得非常多，因此 Subset construction 會將相同的 NFA State set 合併成一個 DFA State。

a DFA state ≡ a set of NFA states
- Find the inital state in the DFA
- Find all the states in the DFA
- Construct the transition table
- Find the final state of the DFA

例如一個 NFA 有 3 個 State，那麼他的 DFA 最多會有 2³ = 8 個 State 才能表示所有的 NFA State set，
但是在實際的語言處理中通常不會看到這種指數增長，並非所有的 NFA State 組合都會出現在實際的輸入序列中。

Algorithm 3.20 : The subset construction of a DFA from an NFA. from Compiler: Principles, Techniques, and Tools p.153
- Input: An NFA N.
- Output: A DFA D with states Dstates and trasition table Dtran

begin
add ε-closure(s0) as an unmarked state to Dstates;
while there is an unmarked state T in Dstates do begin
    mark T;
    for each input symbol a do begin
        U := ε-closure(move(T, a));
        if U is not in Dstates then
            add U as an unmarked state to Dstates;
        Dtran[T, a] := U;
    end;
end;

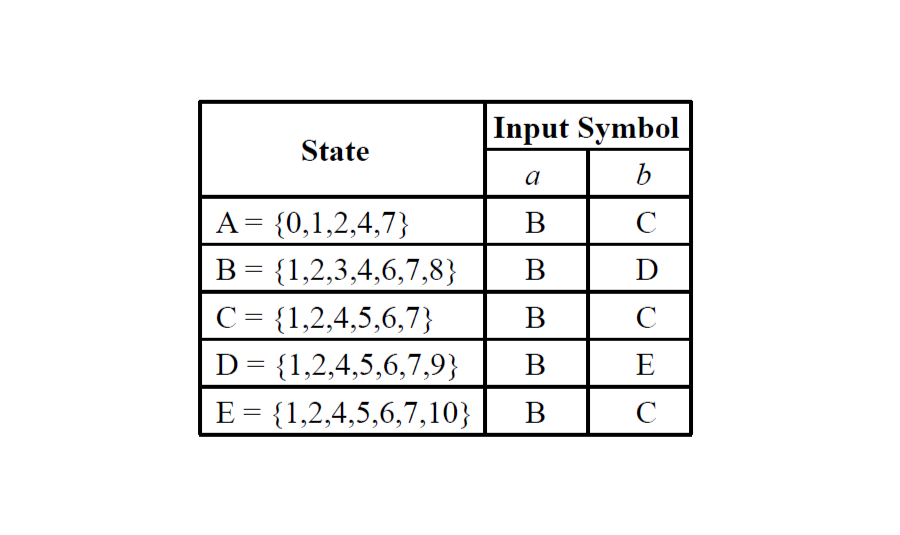
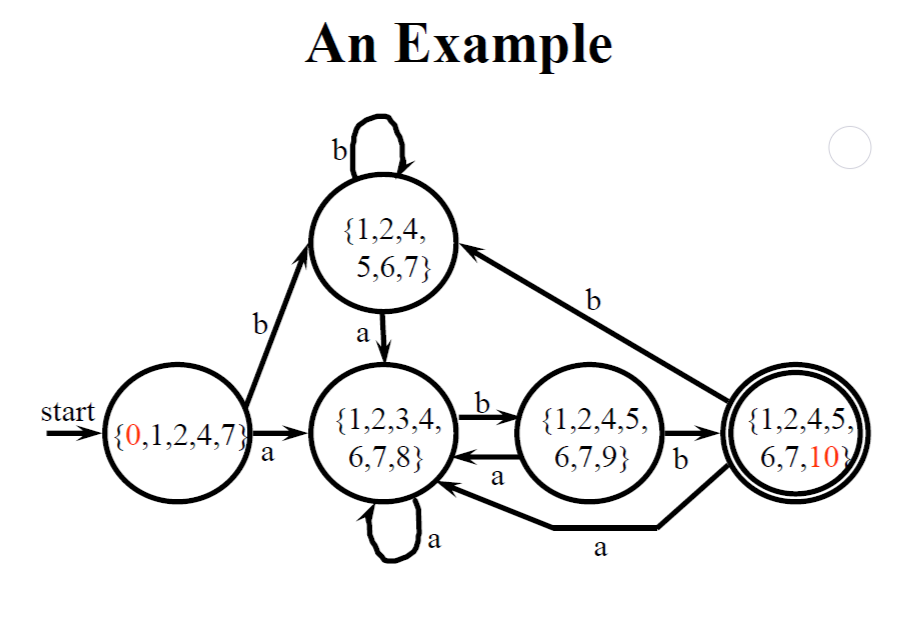
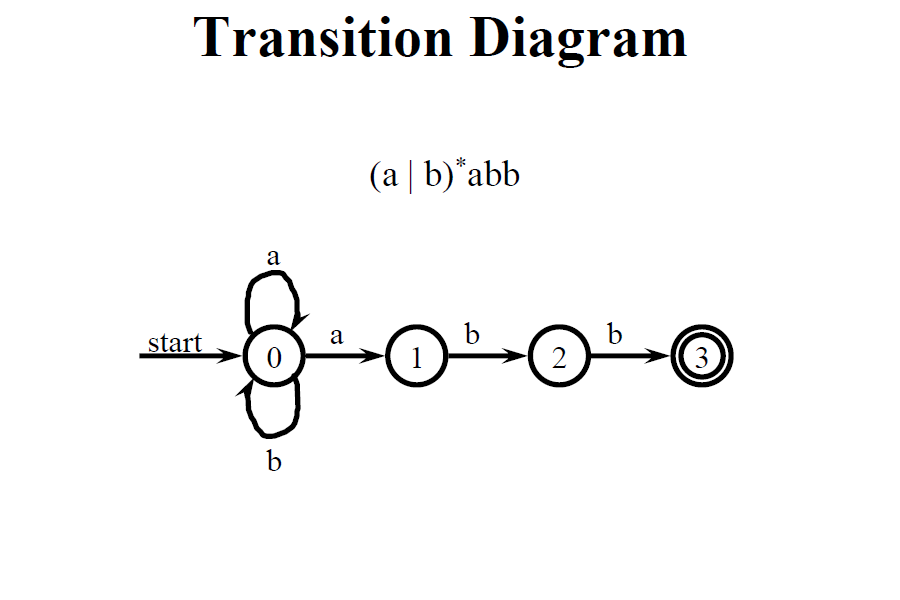
上面是一個將 NFA 轉換為 DFA 的例子

透過 ε-closure(), move($state, $symbols) 找出所有的 NFA State set
將相同的 NFA State set 合併成一個 DFA State
這樣就能透過 DFA State 來繪製出一張 DFA

3.7.3 Tiem Space Tradeoffs

RE to NFA, simulate NFA
- time: O(|r| * |x|), space O(|r|)
RE to NFA, NFA to DFA, simula
- time: O(|x|), space: O(2^|r|)
Lazy transition evaluation
- transitions are computed as needed at run time; computed transitions are stored in cache for later use.

Lazy evaluation(惰性求值)，目的是要最小化計算機要做的工作。可以在空間複雜度上得到極大的優化，從而可以輕易構造一個無限大的數據類型。

Last Edit

10-02-2023 17:50

results matching ""

No results matching ""

, Compiler