October 10, 2023

Testing | Test Case Generation

Software testing course notes from CCU, lecturer Nai-Wei Lin.
Test case 的產生方式可能是無窮無盡的，因此也需要一些策略來幫助產生 Test case

以下是本章節主要介紹的目標，這個章節最後的基於限制式的測試會使用 ECLiPSeclp 來進行實作，不會在這裡介紹，會另外開一篇講述如何使用 Constraint Logic Programming 來生成測試案例。

Test case generation
Equivalence class partitioning
Boundary value analysis
Domain specific information
Constraint-based testing
Test case generation 的目標是從可能無窮(possibly infinite) Collection of candidate test cases，選出盡可能少(Few)並且有效(Effective)的 Test case
Domain knowledge 在測試特定領域的應用時能起到非常關鍵的作用

Two Main Issues

這就涉及兩個主要的問題，可以透過一些原則來解決:

Few(少): 對 Input domains 所有的 Value 進行測試是不可能的，我們只能挑選一部分的 Subset 來測試
- Equivalence class partitioning(等價類別劃分)
- Test coverage criteria(測試覆蓋標準)
Effective(有效): 我們希望選擇一個 Subset，能夠找到最多的 Errors
- Boundary value analysis(邊界值分析)

拿一元二次方程式為例，公式解為:

$ax^2 + bx + c = 0$, $r = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

將每個 Input variable 以 float(32 bit) 表示，所有可能的輸入值數量將會是:

$2^{32} + 2^{32} + 2^{32} = 2^{96}$

3.1 Equivalence Class Partitioning

一組精心選擇的輸入值應該能夠覆蓋許多其他輸入值
這代表我們應該把 Input domains(輸入域) 劃分為有限數量的 Equivalence classes(等價類別)
而測試每個 Equivalence class 中的 Representative value(代表值) 就等於測試了 Equivalence class 中的所有其他值

3.1.1 Valid and Invalid Equivalence Classes

Equivalence classes 通常透過 Input constratint(輸入限制) 來劃分 Input domain(輸入域)
這裡會有兩種 Equivalence classes，Valid 和 Invalid
- Valid: 代表程式的有效輸入
- Invalid: 代表所有其他可能的狀態

An Example:

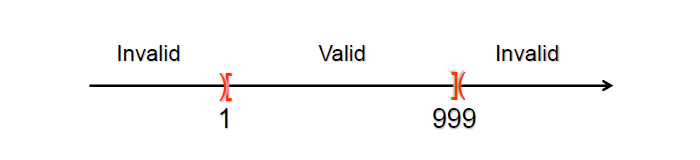
If an input constraint specifies a range of values (e.g., the count can be from 1 to 999), it identifies one valid equivalence class (1 ≤ count ≤ 999) and two invalid equivalence classes (count < 1 and count > 999)

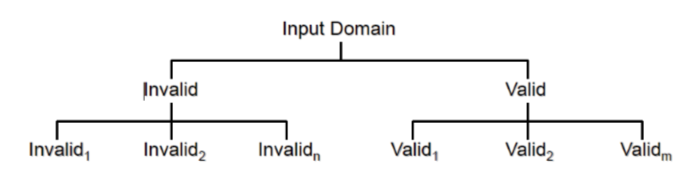
3.1.2 Partitioning Equivalence Classes

如果程式中的 Valid/Invalid Equivalence classes 並不被程式以相同方式處理，則需要劃分更多的 Equivalence classes
如果我們有一個輸入年齡 Y 的程式:
- Invalid: 的輸入可能會被劃分為 Y < 0 和 Y > 1000 (因為根本不會有人活到 1000 歲)
- Valid: 我們也可以把 Y > 65 跟 Y <= 65 區分開來，因為大於 65 歲的退休人士可能有不同的行為
- 這樣我們就在 Invalid/Valid 中另外劃分了 2 個 Equivalence classes

An Example: 回到一元二次方程式為例，方程式的解取決於:

$d = b^2 - 4ac$
$The\;equation\;has\;two\;different\;real\;roots\;if\;d>0$
$The\;equation\;has\;two\;identical\;real\;roots\;if\;d=0.$
$The\;equation\;has\;no\;real\;root\;if\;d<0.$

將一元二次方程式依照 Root 的情況劃分為三種 Equivalence class，這樣就能在這三種情況下挑選 a, b, c 的代表值

3.1.3 Input Space, Vectors, Points

Input Space: Let x1, x2, …, xn denote the input variables. Then these nvariables form an n-dimensional space that we call input space.
Input Vector: The input space can be represented by a vector X, we call input vector, where X = [x1, x2, …, xn].
Test Point: When the input vector X takes a specific value, we call it a test pointor a test case, which corresponds to a point in the input space.

假如有一個 Function，接受兩個 Variable x, y，所有的可能輸入值就會是一個 Input Space，那麼我們的 Input Vector 就是這個 2D 平面上的所有點，而 Test Point 就是這個我們選擇進行測試的點

3.1.4 Input Domain and Sub-Domain

Domain: The input domainconsists of all the points representing all the allowable input combinations specified for the program in the product specification.
Sub-Domain: An input sub-domainis a subset of the input domain. In general, a sun-domain can be defined by a set of inequalitiesin the form off(x1, x2, …, xn) < K, where “<” can also be replaced by other relational operators.

Domain 就是在程式規格允許下的所有輸入值，而這些輸入值可以被程式中的不等式所劃分為 Sub-Domain

Input Domain Partitioning

An input domain partitioningis a partition of the input domain into a number of sub-domains.
These partitioned sub-domains are mutually exclusive, and collectively exhaustive.

例如: 整數輸入可以被劃分為三個 Sub-Domain，n < 0, n = 0, n > 0，這三個 Sub-Domain 互斥且完全涵蓋了整個整數 Domain

3.2 Test Coverage Criteria

如果 Equivalence classes 的數量還是太多，那我們就需要 Test coverage criteria(測試覆蓋標準)來限制 Test Case 的數量，在這裡我們還不會詳細談有哪幾種 Test coverage criteria。

Test Case Candidates Reduction: 下圖是一個減少 Test Case 的流程

3.3 Boundary Value Analysis

邊界上的測試案例通常是最有效的，因為邊界是最容易找到錯誤的地方

A boundaryis where two sub-domains meet.
A point on a boundary is called a boundary point.
Boundary points are input values with the highest probability of finding the most errors.

3.3.1 Definition of boundaries

Linear Boundaries and Sub-Domains

A boundary is a linear boundaryif it is defined by: $a_1x_1+ a_2x_2+ … + a_nx_n = K$ Otherwise, it is called a nonlinear boundary.
A sub-domain is called a linear sub-domainif its boundaries are all linear ones.

Open and Closed Boundaries

A boundary is a closedone with respect to a specific sub-domain if all the boundary points belong to the sub-domain (<=, >=, =).
A boundary is an openone with respect to a specific sub-domain if none of the boundary points belong to the sub-domain (>, <, !=).
A sub-domain with all open boundaries is called an open sub-domain; One with all closed boundaries is called a closed sub-domain; otherwise it is a mixed sub-domain

如果一個邊界的 Point 在 Domain 中，那麼這個邊界就是 Close 的，否則就是 Open 的，例如:

Domain 1 < x <= 100
- 邊界 1 並不屬於 Domain，因此這個邊界是 Open 的
- 邊界 100 屬於 Domain，因此這個邊界是 Close 的

Interior and Exterior Points

屬於 Sub-domain 但不在邊界上的點稱作 Interior point
不屬於 Sub-domain 並且不在邊界上的點稱作 Exterior point
而兩條以上的邊界相交的點稱作 Vertex point

General Problems with Input Values

Some input values cannot be handled by the program. These input values are under-defined.
Some input values result in different output. These input values are over-defined.
These problems are most likely to happen at boundaries.
Under-defined input values(未定義的輸入值): 也就是程式無法處理的 Input value，例如: 除以零
Over-defined inpyt values(過度定義的輸入值): 也就是程式可以處理但是可能有不同輸出的 Input value，例如: 一個投票系統，可能會因為地方的法律而有不同的投票年齡限制

3.3.2 Boundary Problems

這裡列出 5 個主要的 Boundary Problems:

Closure Problem(閉合問題): whether the boundary points belong to the sub-domain.
Boundary shift/tilt Problem: where exactly a boundary is between the intended and the actual boundary.
- Boundary shift Problem: f(x1, x2, …, xn) = K, where a small change in K.
- Boundary tilt Problem: f(x1, x2, …, xn) = K, where a small change in some parameters.
Missing/Extra boundary Problem:
- Missing: a boundary missing means that two neighboring sub-domains collapse into one sub-domain.
- Extra: An extra boundary further partitions a sub-domain into two smaller sub-domains.

3.4 Test Case Generation Strategy

Weak N x 1 / 1 x 1 Strategy 都是一種用於邊界測試的策略，這裡會介紹這兩種策略的差異與優缺點

3.4.1 Weak N x 1 Strategy
3.4.3 Weak 1 x 1 Strategy

3.4.1 Weak N x 1 Strategy

In an n-dimensional space, a boundary defined by a linear equationin the form off (x1, x2, …, xn) = K would need nlinearly independent pointsto define it.
We can select nsuch boundary points, called ON points, to precisely define the boundary.
We can also select a point, called an OFF point, that receives different processing.

The OFF Points

閉合的邊界: 那麼它的 Off point 會位邊界的外部
開放的邊界: 那麼他的 On point 會位邊界的內部
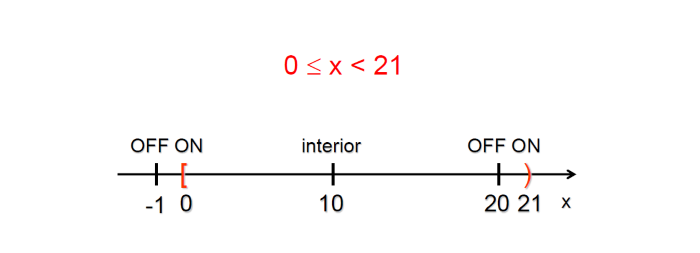
0 <= N < 21 在這個例子上有兩個邊界，其中 0 是 Close boundary、21 是 Open boundary
- ON Points 是 0, 21 這兩個位於邊界上的點
- 0 是 Close boundary, Off point -1 位於外側
- 20 是 Open boundary, Off point 20 位於內側

Distance of the OFF Points

需要 Off point 的理由是，他與邊界非常的接近，以至於邊界的細微變化都將影響 Off point 的處理
實際應用上，使用 distance ε 作為 Off point 與邊界的偏移距離
- For integers, ε = 1.
- For numbers with nbinary digits after the decimal point, ε = 1/2ⁿ.

例如: 有一個 0.001 作為邊界值，那麼 ε 就是 1/2³ = 1/8

Position of the OFF Points

Off point 應該要位於所有 On point 的中央
對於一個 2D 的空間來說，他應該選擇的方式如下:
- 選擇位於兩個 On point 的中點
- 根據這個邊界是 Closed 或 Opend 向外或向內移動 ε 的距離

Total Test Points

除了 ON/OFF Points 我們也會再選擇一個 Interior Point(內部點)做為該 Equivalence Class(Sub-Domain) 的代表，因此一個 N Dimensional domain 將會有 (n + 1)*b + 1 個 Test Points。

Example:
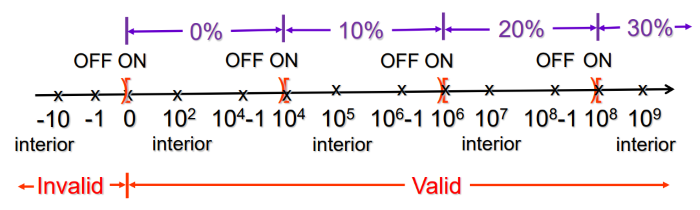
假設有一個稅收級距如下，注意其中 Close 與 Open 的條件，這裡都是 Integers 這樣的話旁邊的 Sub-Domain OFF Points 剛好會重疊在一起可以省略掉，並且 Open domain 也可以省略一個邊界的值，因此原本應該要有 3 * 2 + 5 * 3 = 21 個點，但是有 4 個邊是重疊的因此 21 - 4 * 2 = 13，最終僅用上 13 個 Test Points。

Tax Rate:
0%:  0 <= x < 10000 (0~9999)
10%: 10000 <= x < 1000000 (10000~999999)
20%: 1000000 <= x < 100000000 (1000000~99999999)
30%: x <= 100000000 (100000000~)

那如果假設一個 2D Sub-domain，並且四個邊都是封閉的，將會是 (2 + 1) * 4 + 1 = 13 個 Test Points，這裡忽略了與旁邊的 Sub-domain 重疊的點

3.4.2 Boundary Problem Detection of Werk N * 1 Strategy

這裡說明 Weak N x 1 Strategy 在處理 Boundary Problem 時能做到什麼，不能做到什麼

Closure problem
- 定義邊界是是否所有可能的邊界都被包含在內
Boundary shift problem
- 邊界是否有正確設置在應該的位置
Boundary tilt problem
- 邊界是否有正確的對齊或平行
Missing boundary problem
- 是否所有的邊界都有被定義
Extra boundary problem
- 是否有多餘的邊界

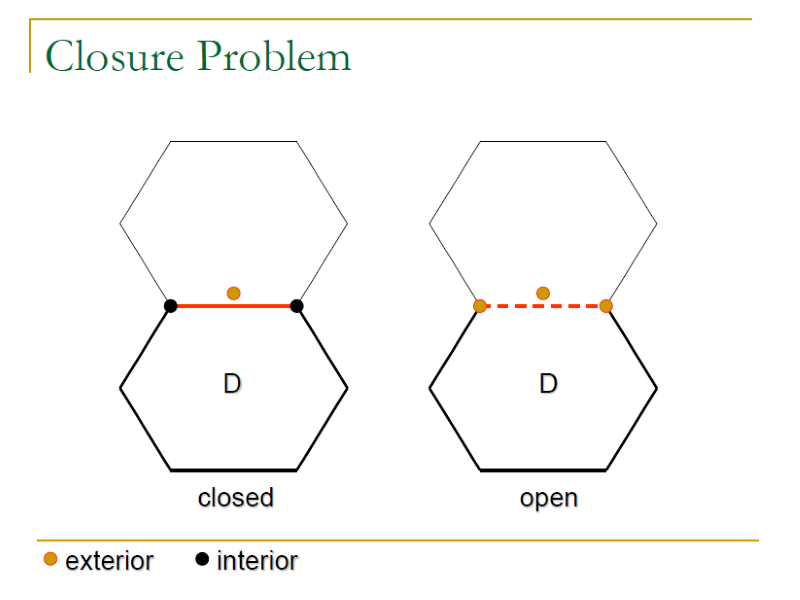
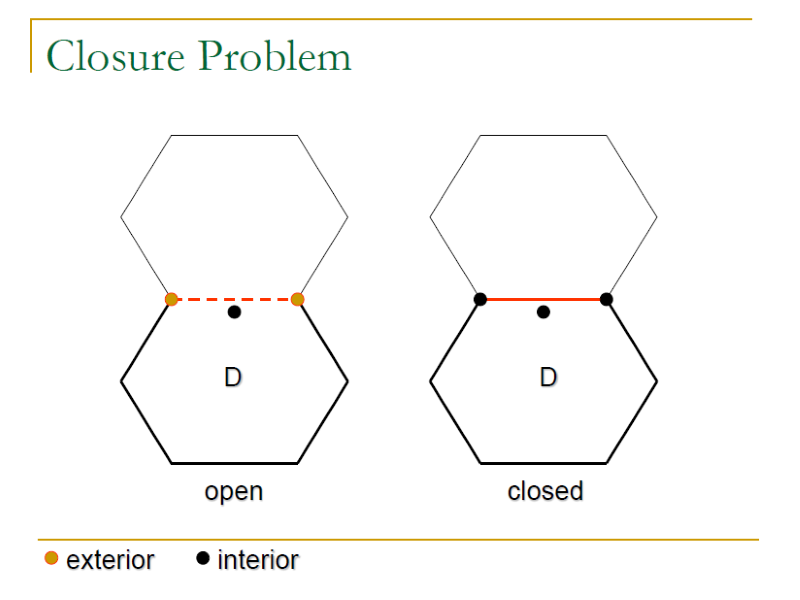
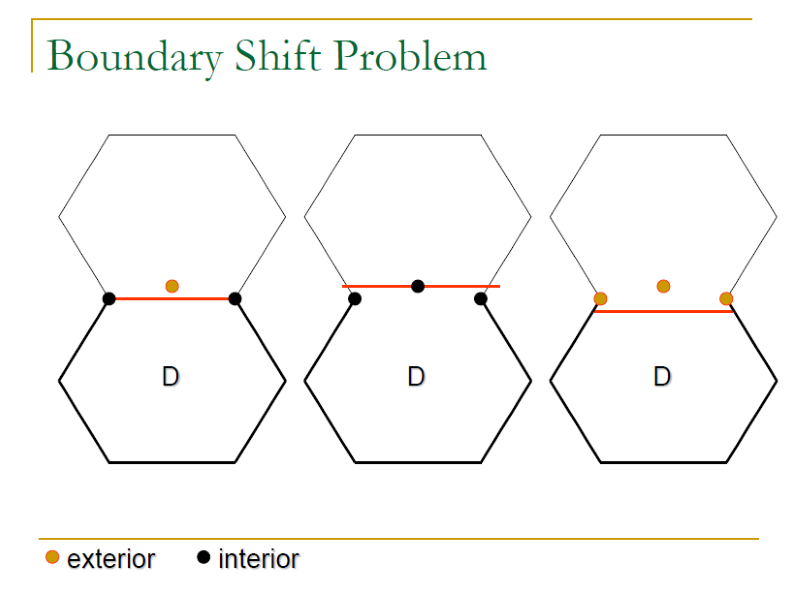
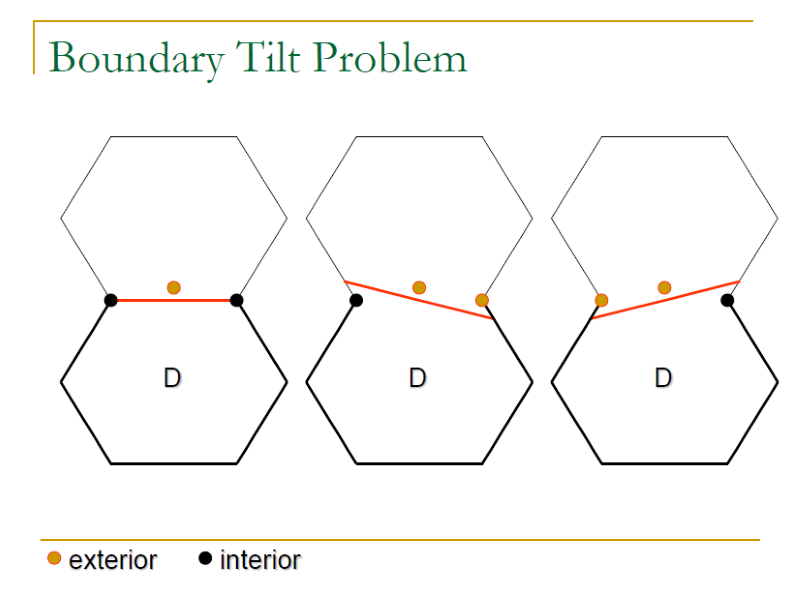
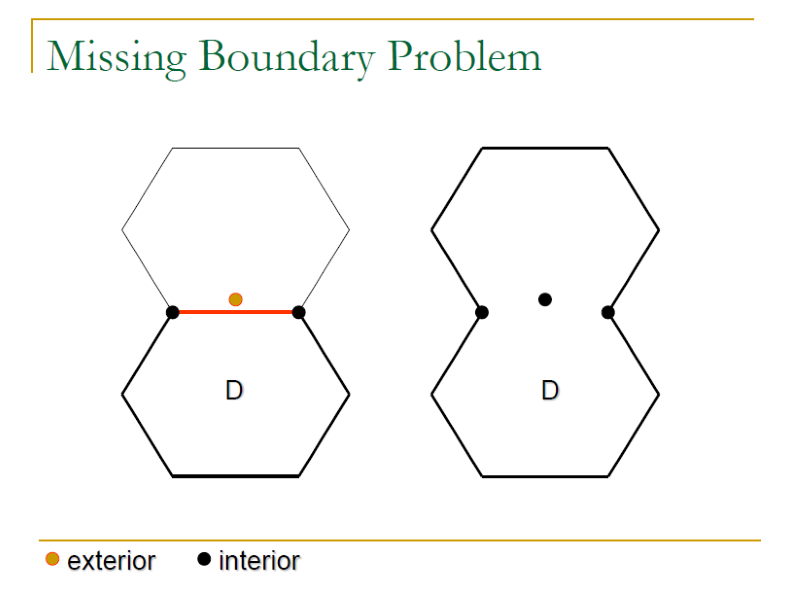
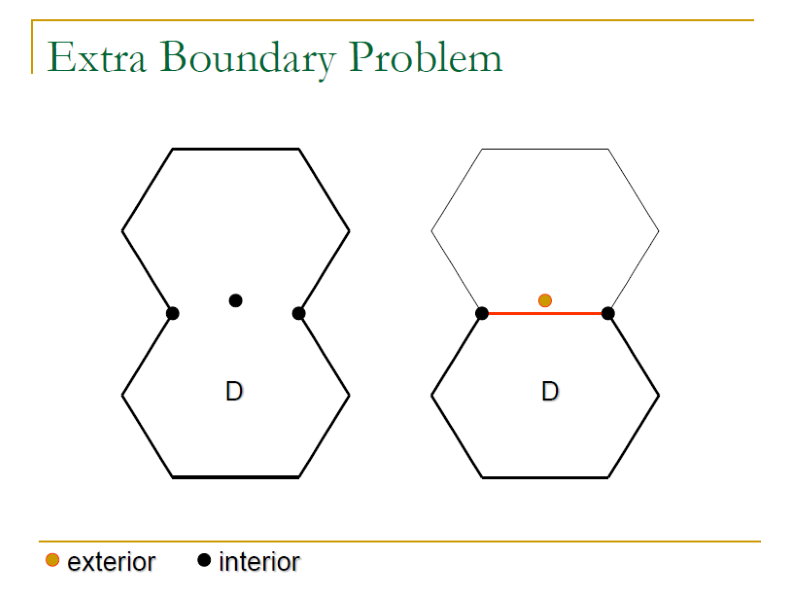
Weak N x 1 Strategy 可以很好的處理其他 Boundary problem 但無法完全偵測到 Extra boundary problem

3.4.3 Weak 1 x 1 Strategy

Weak 1 x 1 Strategy 在每個邊界上只放置一個 On point 與一個 Off point，減少 Test Points 數量，但是也會有缺點

One of the major drawbacks of weak N x 1 strategy is the number of test points used, (n+1)xb+1 for ninput variables and boundaries.
Weak 1 x 1 strategy uses just one ON point for each boundary, thus reducing the total number of test points to 2xb+1.
The OFF point is just ε distance from the ON point and perpendicular to the boundary.

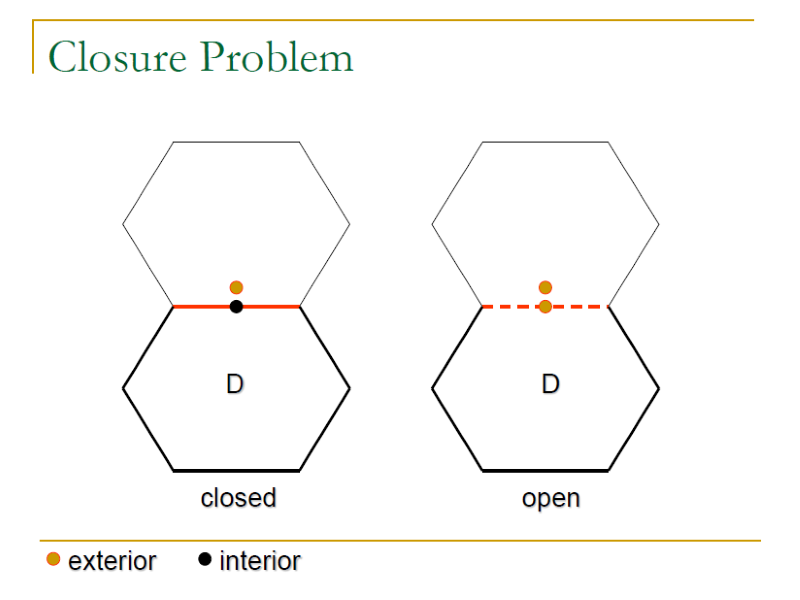
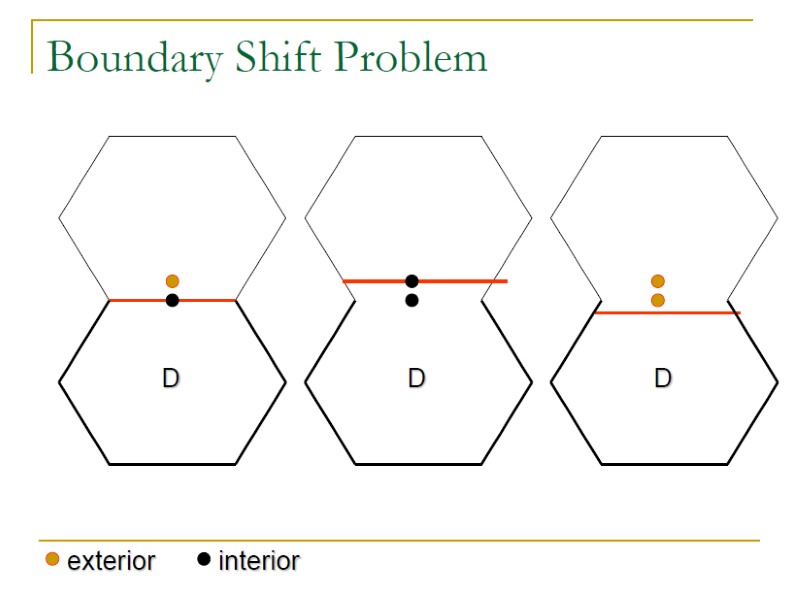
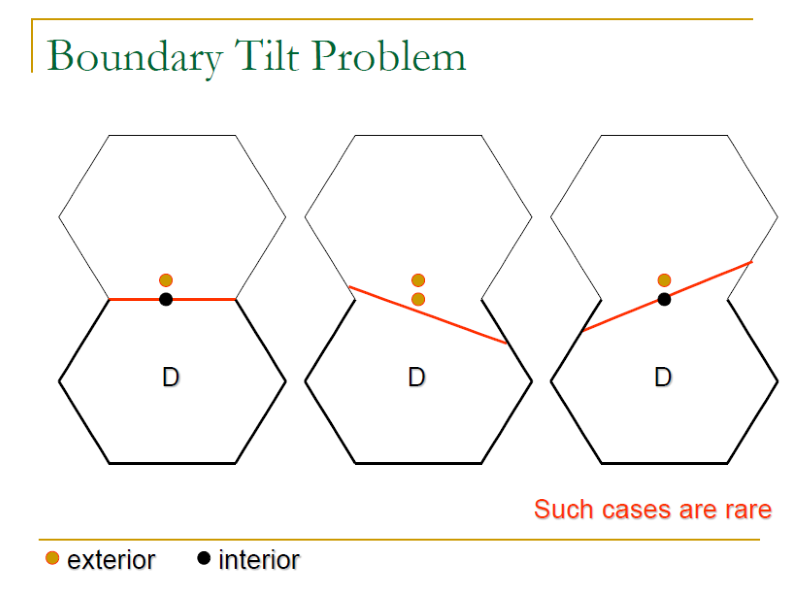
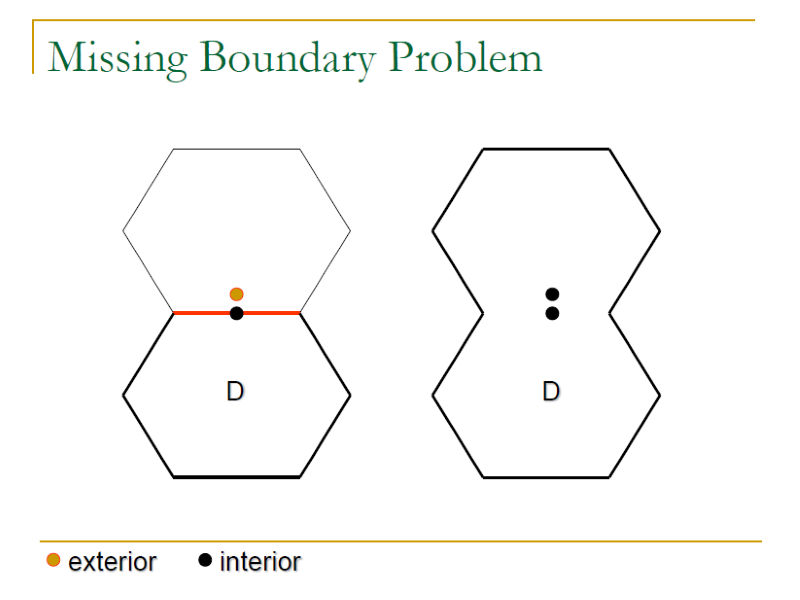
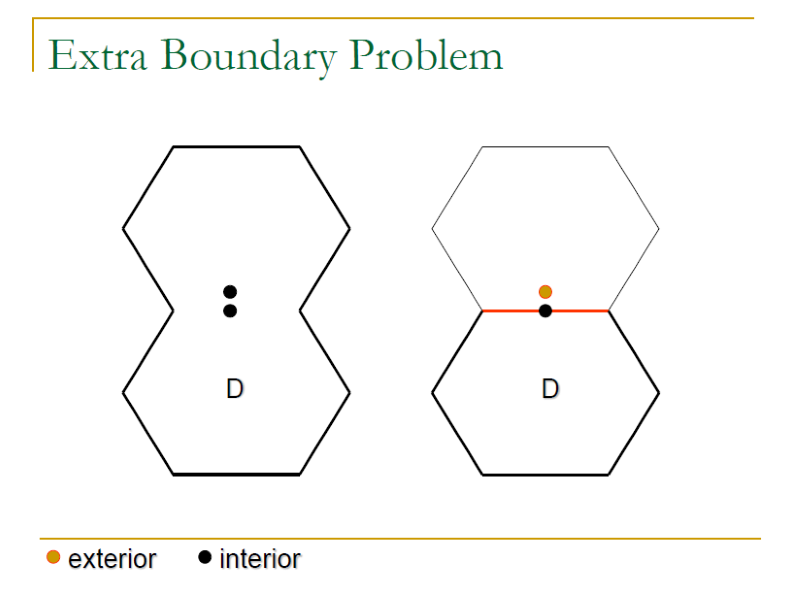
Weak 1 x 1 Strategy 也可以處理 Boundary Problem，但是在傾斜上的表現不如 Weak N x 1 Strategy，並且跟 Weak N x 1 Strategy 一樣無法完全偵測到 Extra boundary problem

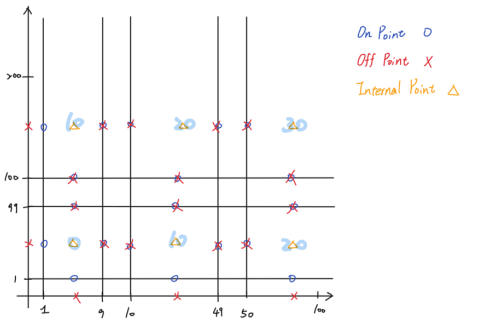
在 2D 平面上比較能表示出兩種策略的差異，可以看到 Weak N x 1 Strategy 在同個 Domain 的邊界上會有 3 個 Points，而 Weak 1 x 1 Strategy 則只有 2 個 Points，下圖左右分別是 Weak N x 1 Strategy 和 Weak 1 x 1 Strategy:

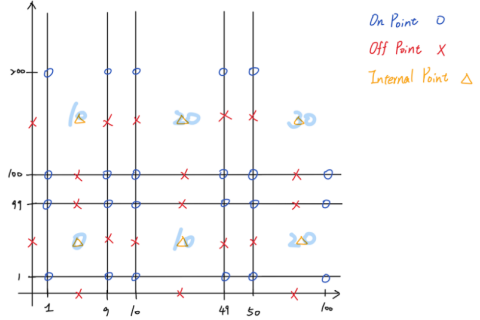
3.5 Looking for Equivalence Classes

找尋 Equivalence Classes(等價類別)的方法與需要注意的點

Don’t forget equivalence classes for invalid inputs.
Organize your classifications into a table or an outline.
Look for ranges of numbers.
Look for membership in a group.
Analyze responses to lists and menus.
Look for variables that must be equal.
Create time-determined equivalence classes.
Look for variable groups that must calculate to a certain value or range.
Look for equivalent output events.
Look for equivalent operating environments.

Don’t Forget Equivalence Classes for Invalid Inputs

通常 Invalid Inputs 是最容易產生 Bugs 的來源
例如一個能接受 1 到 99 之間任何數字的程式，那就至少有四個 Equivalence Classes
- 1 >= x <= 99
- x < 1
- x > 99
- Not a number(Is this true for all non-numbers?)

Organize Your Classifications into a Table or an Outline

把分類整理成表格或者大綱

會發現有這麼多的 Input/Output constraints，跟相關的 Equivalence Classes，需要一種組織方法
最常用的方法就是 Table(表格)或者 OutLine(大綱)

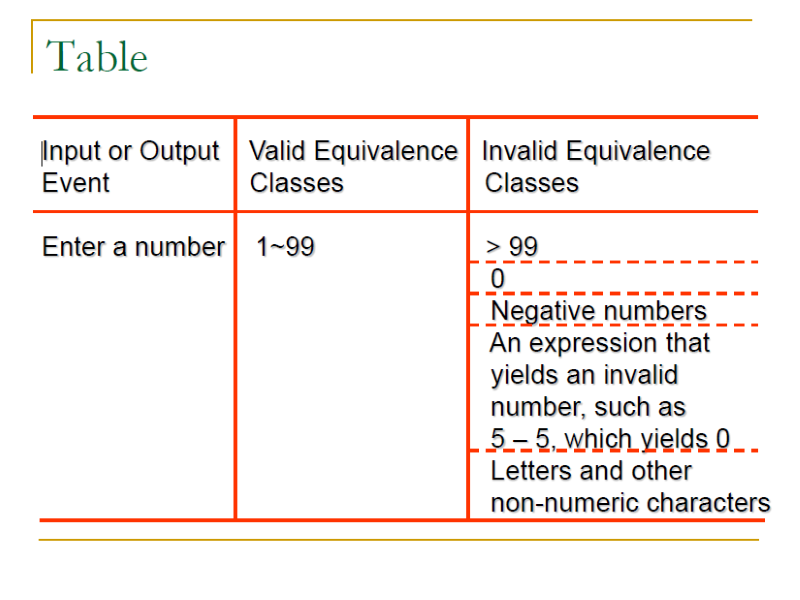
Look for Ranges of Numbers

如果找到一個數字的範圍，例如: 1 到 99，這些範圍就是 Equivalence Classes
通常會有三個 Invalid Equivalence Classes，小於 1、大於 99、以及不是數字的情況
當然也會有多個範圍的情況，例如: Tax

Look for Membership in a Group

如果一個 Input 必須屬於某個 Group，那麼一個 Equivalence Class 則包含該 Group 的所有成員
而另一個 Equivalence Class 則包含所有不屬於該 Group 的成員
例如: 要求輸入一個國家的名稱，Valid Equivalence Class 就是所有國家的名稱，Invalid Equivalence Class 就是所有不是國家的名稱
但是，abbreviations(縮寫)、almost correct spellings(幾乎正確的拼寫)、native language spellings(母語拼寫)、name that are now out of date but were country names(曾經存在過的名稱)又該如何處理?
- 應該分別測試這些情況嗎?
- 通常 Specification 不會提到這些情況，但是在測試中可能會發現這些錯誤

Analyze Responses to Lists and Menus

對於必須從 List 或 Menu 中選擇的 Input，每個選項都是一個 Equivalence Class
每個 Input 都是其自身的 Equivalence Class
Invaild Equivalence Class 則是所有不在 List 或 Menu 中的選項
例如: “Are you sure? (Y/N)”，一個 Equivalence Class 就是 Y，另一個 Equivalence Class 就是 N，Invalid Equivalence Class 就是其他所有選項

Look for Variables That Must Be Equal

例如一個可以輸入任何顏色的程式，但必須是黑色，那麼所有的顏色都是 Invalid Equivalence Class，而黑色就是 Valid Equivalence Class
有時這種限制在實際應用中可能會出現意外情況: 例如黑色已售罄，只剩下其他顏色
這種曾經有效但現在不再有效的選擇，應該為它們建立一個 Equivalence Class

例如: 在閏年時 February 有 29 天，但是在非閏年時 February 只有 28 天，這樣就會有兩個 Equivalence Classes

Create Time-Determined Equivalence Classes

例如一個程式還沒有從 Disk 完成讀取，在進行中與結束上按下空格鍵是不同的 Equivalence Classes
這種情況通常會有三個 Equivalence Classes，一個是還沒開始讀取的情況，一個是讀取中的情況，一個是讀取完畢的情況

Look for Variable Groups That Must Calculate to a Certain Value or Range

例如輸入 Triangle 的三個邊長
在 Valid Equivalence Class 中，它們的總和應該等於 180°
而 Invalid Equivalence Class 則會有兩個分別是大於 180° 與小於 180°

Look for Equivalent Output Events

在此之前我們強調的都是 Input 與 Invalid Input，這是因為 Output 通常更複雜，因為通過程式處理後的 Output 會有很多種可能的情況

例如我們有一個由程式控制的繪圖機，他最多可以一次畫 4 公尺的線條
怎麼判斷一個線條是 Valid Equivalence Class 還是 Invalid Equivalence Class?
- 有可能繪製了超過 4 公尺的線條
- 可能根本沒有繪製線條
- 也有可能繪製了根本不是線條的東西，例如: 圓形

在測試中不只要關注輸出的情況，也要關注輸出並找到 Equivalence Classes Of Output

Look for Equivalent Operating Environments

同時對於環境的變化也要找到 Equivalence Classes

例如: 一個程式要求至少要 64K - 256K 的可用 Memory
- 這樣就會有三個 Equivalence Classes，符合規範與小於 64K、大於 256K的情況

Last Edit

10-28-2023 16:46
剩下的部分是 Constraint-based testing，會另外講述如何使用 CLP 來生成測試案例

results matching ""

No results matching ""

, software, software_qualitiy