October 26, 2023

Compiler | Syntax Analysis Notes

Compilers course notes from CCU, lecturer Nai-Wei Lin. Syntax Analysis(語法分析) 在這個階段會檢查 Lexical Analysis 返回的 Token 是否符合語法規則，並且建立語法樹

以下是這個章節的主要大綱，Bison 不會在這篇介紹如何使用，主要是介紹 Syntax analysis 的概念

Introduction to parsers
Context-free grammars
Push-down automata
Top-down parsing
Buttom-up parsing
Bison a parser generator

4.1 Introduction to parsers

本章會先介紹 Parser 在 Compiler 中的作用，然後介紹 Context free grammar。

4.1.1 The Role of the Parser

在編譯器模型中 Systax analysis 從 Lexical analysis 獲取由 Token 所組成的字串，概念上語法分析需要建構一個 Parse tree 傳遞給 Compiler 的其餘部分進行進一步處理，但實際上不一定要真的用一個 Data structure 來建構 Parse tree，而是在 Parsing 的過程中進行 Semantic analysis，並將資訊傳遞給 Compiler 的其餘部分。

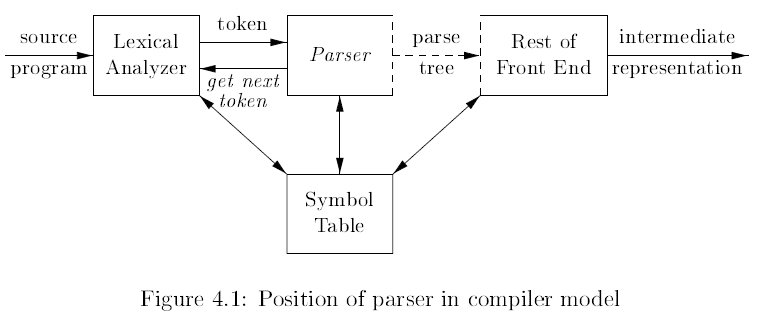
不真正建構一個 Parse tree 通常是為了節省記憶體，但缺點就是他使 Debug 變得困難，因為無法查看 Parse tree

4.2 Context-free grammars

Context-free grammars 可以系統的描述程式語言構造，例如使用 stmt 描述 statements，expr 描述 expressions，那麼:

production: stmt -> if (expr) stmt else stmt

我們就能透過其他 production 來描述 stmt, expr 會是什麼，還可以是什麼?

4.2.1 The Formal Definition of a Context-free Grammar

A set of terminals: basic symbols from which sentences are formed
- 例如: if, else, (, ), id
A set of nonterminals: syntactic categories denoting sets of sentences
- 任何非 terminal 都可以是一個 nonterminal，例如: stmt, expr
A set of productions: rules specifying how the terminals and nonterminals can be combined to form sentences
- 例如: stmt -> if (expr) stmt else stmt
The start symbol: a distinguished nonterminal denoting the language
- 通常是最上層的 Production

Example:

Terminals: id + - * / ( )
Nonterminals: expr op
Productions:

expr -> expr op expr  
expr -> '(' expr ')'  
expr -> '-' expr  
expr -> id  
op -> '+' | '-' | '*' | '/'  
The start symbol: expr  

4.2.2 Notation Conventions

通常為了避免陳述 these are the terminals, these are thenonterminals 會使用一些約定來規範符號:

Terminals:
- 小寫字母，例如: a b c
- 運算符號，標點符號，例如: + - , ( )
- 數字，例如: 0 1 2
- 粗體字符串，例如: if else then
- 小寫希臘字母，例如: α β γ
Non-Terminals:
- 大寫字母，例如: A B C
  - 在討論構造時，例如 expression、terms、factors，使用: E T F
- 通常使用 S 來表示 Start symbol
- 斜體字符串，例如: expr stmt
具有相同標題的 Production 可以使用 | 來分隔，例如: A -> a、A -> b、A -> c 可以寫成 A -> a | b | c
除非特殊說明，第一個 Production 會是 Start symbol

4.2.3 Parse Trees and Derivations

推導(derivation) 步驟是將一個 Production 的替換過程寫出，例如 E => - E
一系列的推導步驟可以將 E => -E => -(E) => -(id)
如果使用 =>^* 表示在零步或多步中推導，=>⁺ 表示在一步或多步中推導
- 例如上面的步驟可以簡化為 E =>^* -(id)

Context free grammar

Context free grammar(CFG) 定義的語言 L(G)，是由 CFG G 所定義的語言
一個 Terminal 字串 ω 在 L(G) 中，並且當 S =>⁺ ω，那我們稱 ω 是 G 的一個句子(sentence)
如果 S =>^* α，而 α 可以包含 Non-terminal，那麼 α 是 G 的一個句型(sentence form)
如果 L(G1) = L(G2)，那麼 G1 和 G2 是等價的(equivalent)

Left & Right-most Derivations

每個 Derivation step 都需要兩個步驟:

選擇替換哪個 Terminal
替換後選擇一個以此 Terninal 作為開頭的 Production

這樣就可以有 Left & Right 兩種推導方式:

Left-most derivation: 每次都選擇最左邊的 Terminal 來替換
- 例如 E =>_lm -E =>_lm -(E) =>_lm -(E+E) =>_lm -(id+E) =>_lm -(id+id)
Right-most derivation: 每次都選擇最右邊的 Terminal 來替換
- 例如 E =>_rm -E =>_rm -(E) =>_lm -(E+E) =>_lm -(E+id) =>_lm -(id+id)

Exercise 4.2.1:

Consider the following grammar:
S -> SS+ | SS* | a
and the string aa+a*

(a), Giver a leftmost derivation for the string.
(b), Giver a rightmost derivation for the string.

(a) S =>lm SS* => SS+S* => aS+S* => aa+S* => aa+a*
(b) S =>rm SS* => Sa* => SS+a* => Sa+a* => aa+a*

4.2.4 Parse Trees and Derivations

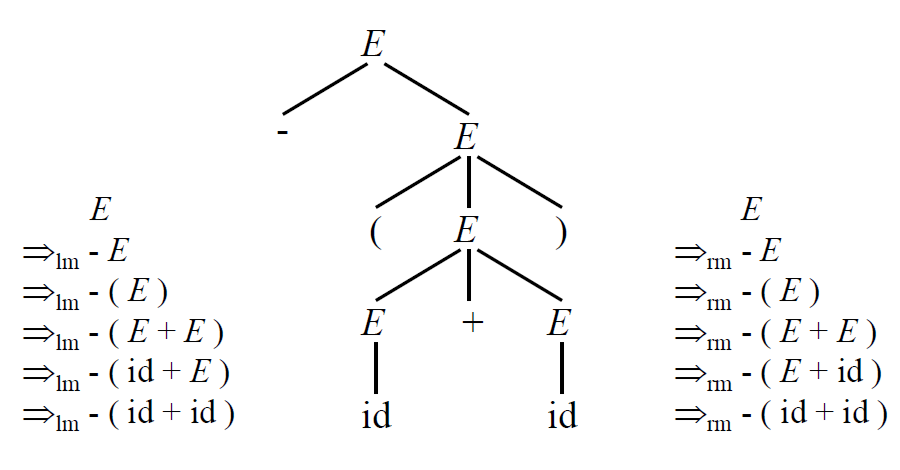
Parse Tree 是推導的圖形表示，顯示了從 Start symbol 到衍生 Sentence 的過程，這種方式過濾了選擇 Terminal 進行重寫的順序
因此不管是 Left/Right-most 都應該推導出相同的 Parse tree

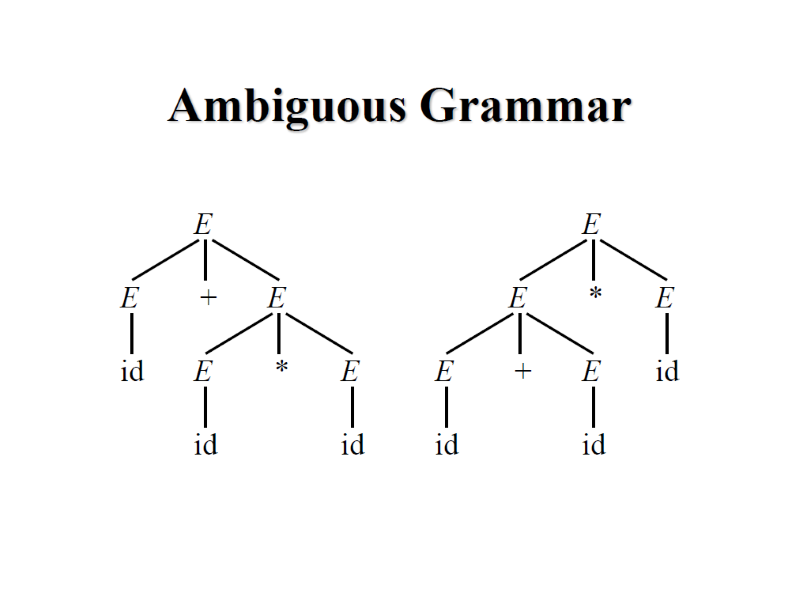
4.2.5 Ambiguous Grammar

如果一個 Grammar 可以對同一個 Sentence 產生不同的 Parse tree 那就是 Ambiguous

Resolving Ambiguity

大部分的 Syntax analysis 都希望 Grammar 不是 Ambiguous，可以透過以下來消除

Use disambiguiting rules to throw away undesirable parse trees
Rewrite grammarsby incorporating disambiguiting rules into grammars

Example

The dangling-else grammar

stmt -> if expr then stmt
    | if expr then stmt else stmt
    | other

如果用以上的 Grammar 來分析:

if E₁ then if E₂ then S₁ else S₂

我們無法確定 else 是對應哪個 then，因此會產生兩個 Parse tree

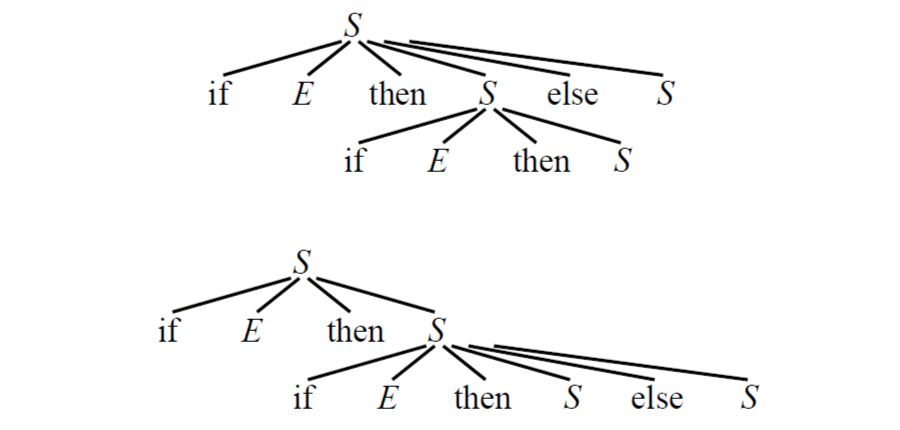
這樣就產生了兩個 Parse tree，因為在語法規則中沒有說明清楚 else 要對應哪個 if，所以可以透過以下方式來消除

Disambiguiting rules:

Rule: match each else with the closest previous unmatched then
Remove undesired state transitions in the pushdown automaton

stmt -> m_stmt | unm_stmt
m_stmt -> if expr then m_stmt else m_stmt
    | other
unm_stmt -> if expr then stmt | if expr then m_stmt else unm_stmt

透過這種方式，我們強制一個 then 和 else 之間只能是一個 m_stmt，這樣就可以消除 Ambiguous

4.3 Writing a Grammar

4.3.1 Lexical Versus Syntactic Analysis

由 RE 描述的每種語言也可以由 CFG 描述，例如 (a|b)*abb 也可以用 CFG 來描述:

A0 -> aA0 | bA0 | aA1
A1 -> bA2
A2 -> bA3
A3 -> ε

那為什麼不在 Lexical analysis 使用 CFG?
- 首先 Lexical analysis 不需要與 CFG 一樣強大的表示法
- RE 比 CFG 更簡潔更容易理解
- RE 建構的 Lexical analysis 比 CFG 建構的 Lexical analysis 更有效率
- 這樣提供了將前端模塊化為兩個易於管理的部分的方法

Nonregular Constructs

REs can denote only a fixed number of repetitions or an unspecified number of repetitions of onegiven construct: an, a*
A nonregular construct:
- L = {aⁿbⁿ| n ≥ 0}
- 這個語言包含相同數量的 a 和 b，RE 沒辦法描述固定數量的 a 和 b

Non-Context-Free Constructs

CFGs can denote only a fixed number of repetitions or an unspecified number of repetitions of oneor twogiven constructs
Some non-context-free constructs:
- L1 = {wcw | w is in (a|b)*}
- L2 = {aⁿb^mcⁿd^m | n ≥ 1 and m ≥ 1}
- L3 = {aⁿbⁿcⁿ | n ≥ 0}

CFG 只能處理一個重複的結構，這也涉及到 CFG 的 Automata，但是可以描述以下語言:

L1 = {ⁿcⁿ | n ≥ 0}
L2 = {aⁿb^mc^mdⁿ | n ≥ 0, m ≥ 0}

4.4 Top-down Parsing

這裡不會詳細介紹 Top-down Parsing，因為 Top-down 要處理的問題比較多

Top-down Parsing 是從上層的 Root 開始，使用 Leftmost derivation 建構一顆到 Leaf 的 Parse tree

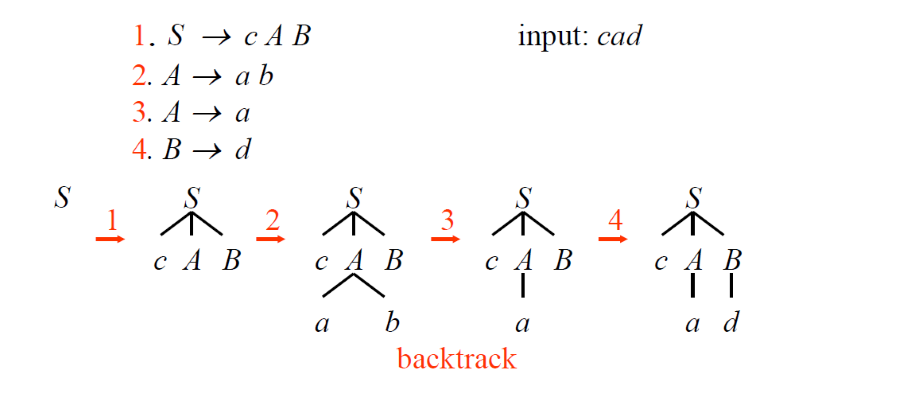
Predictive Parsing

A top-down parsing without backtracking – there is only one alternative production to choose at each derivation step

stmt -> if expr then stmt else stmt
    |  while expr do stmt
    |  begin stmt_list end

4.4.2 FIRST and FOLLOW Sets

First set

The first setof a string α is the set of terminals that begin the strings derived from α. If α =>* ε, then ε is also in the first set of ε.
如果 X 是一個 Terminal，那麼 FIRST(X) = {X}
如果 X 是一個 Nonterminal，並且存在 X -> ε，那麼 FIRST(X) = {ε}
如果 X 是一個 Nonterminal，並且存在 X -> Y₁ Y₂ … Y_n
1. 首先加入 FIRST(Y_i) 如果 Y_i 存在 ε，那就加入 FIRST(Y_i) - {ε}
2. 然後 i + 1 重複以上步驟直到 Y_i 不存在 ε

簡單來說 FIRST 就是找出一個 Nonterminal 所有可能的開頭 Terminal

Example:

E  -> TE'
E' -> +TE' | ε
T  -> FT'
T' -> *FT' | ε
F  -> (E) | id

FIRST(E)  = { ( , id }
FIRST(E’) = { +, ε }
FIRST(T)  = { ( , id }
FIRST(T’) = { *, ε }
FIRST(F)  = { ( , id }

這裡舉 FIRST(E) 為例子，從 E 開始不斷往下找直到找到 Terminal，E -> T -> F -> { (, id }

Follow set

The follow setof a nonterminal A is the set of terminals that can appear immediately to the right of Ain some sentential form, namely, S =>* αAaβ, a is in the follow set of A.

如果對 Start symbol 尋找 FOLLOW(S) 要先加入 { $ }
如果存在 Production A -> αB
- FOLLOW(B) 包含 FOLLOW(A)
如果存在 Production A -> αBβ
- FOLLOW(B) 包含 FIRST(β) - {ε}
如果存在 Production A -> αBβ，並且 FIRST(β) 包含 ε
- FOLLOW(B) 包含 { FIRST(β) - {ε} } U FOLLOW(A)

簡單來說 FOLLOW 就是找出一個 Nonterminal 所有可能的結尾 Terminal

Example, Using previous grammar:

FOLLOW(E)  = { $ } U FIRST( ')' )
           = { $, ) }
FOLLOW(E') = FOLLOW(E)
           = {  $, ) }
FOLLOW(T)  = { FIRST(E') – ε } U FOLLOW(E') U FOLLOW(E)
           = { +, $, ) }
FOLLOW(T') = FOLLOW(T)
           = { +, $ , ) }
FOLLOW(F)  = { FIRST(T') –  ε } U FOLLOW(T')
           = { *, +, $, ) }

這裡以 FOLLOW(F) 為例: T' -> *FT' 跟 T -> FT' 這兩處出現 F，但後面跟著的都是 T’，先做 T' -> *FT'

因此 FIRST(β) = FIRST(T’) = { *, ε }

此處出現 ε，因此要依照規則 4 把 FOLLOW(T’) 加入 FOLLOW(F)

因此變成 { FIRST(T') - ε } U FOLLOW(T') = { *, +, $, ) }

4.5 Bottom-up Parsing

Bottom Up Parsing 是從底層的 Leaf 開始，使用 Rightmost derivation 建構一顆到 Root 的 Parse tree

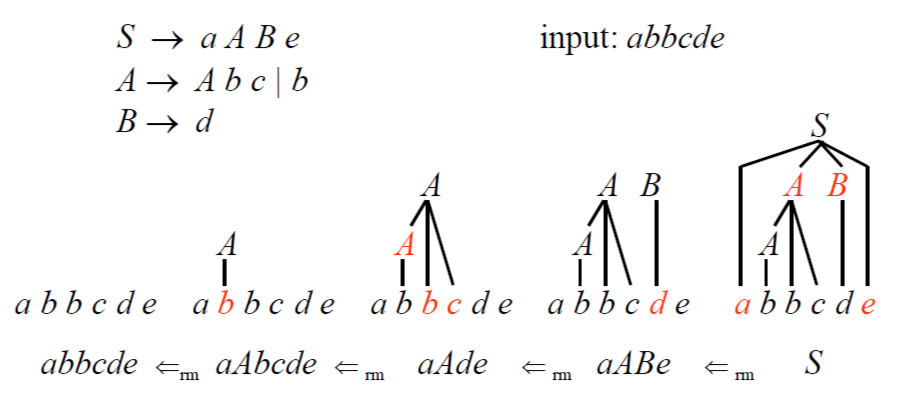
Handles

A handle β of a right-sentential form γ consists of
- a production A -> β
- a position of γ where β can be replaced by A to produce the previous right-sentential form in a rightmost derivation of γ

非正式的講 handle 就是和某個 Production 能匹配的 Substring，對他化簡就代表反向的 Rightmost derivation

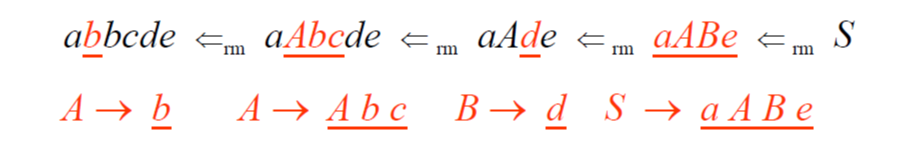
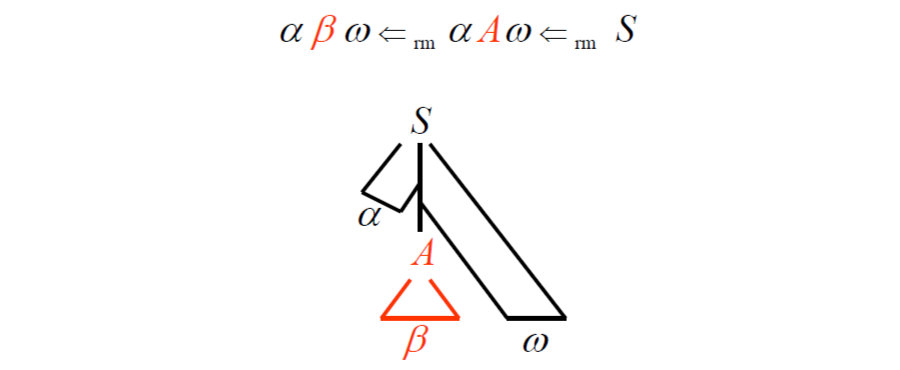
The string ω to the right of the handle contains only terminals
Ais the bottommost leftmostinterior node with all its children in the tree

如果有 S =>^* αAω => aβω，那麼緊跟在 a 之後的 Production A -> β 就是 aβω 的一個 Handle，要注意 ω 一定只包含 Terminals，如果 grammmr 是 Non-amibiguous，那麼 aβω 只會有一個 rightmost derivation，否則可能會有多個。

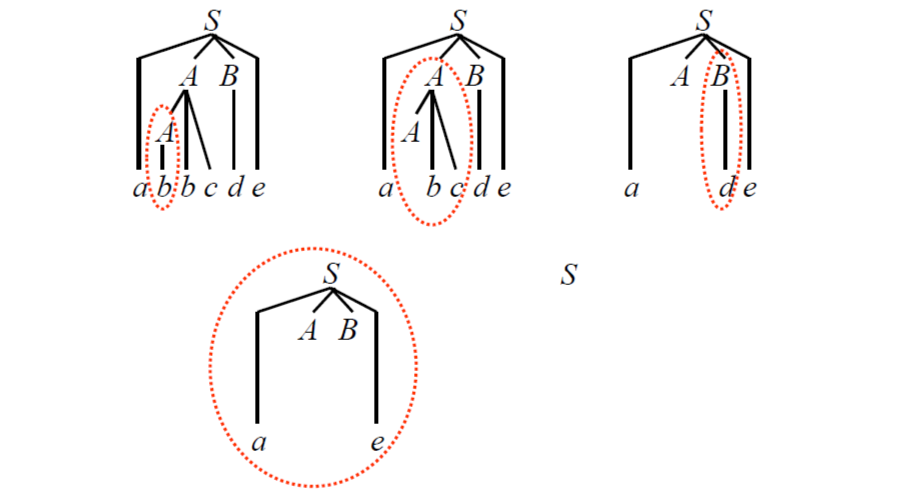
Handle pruning: 就是一個 Parse tree 識別 Handles 並將他們替換為 Nonterminal，到最後的過程

4.5.3 Shift-Reduce Parsing

因此 Bottom-Up Parsing 又稱為 Shift-Reduce Parsing，因為他們的過程就是不斷的 Shift 和 Reduce

Shift: shift the next input symbolonto the top of the stack
Reduce: replace the handle at the top of the stack with the corresponding nonterminal
Accept: announce successful completion of the parsing
Error: call an error recovery routine

例如之前的例子，其實就是一個不斷 Shift 和 Reduce 的過程:

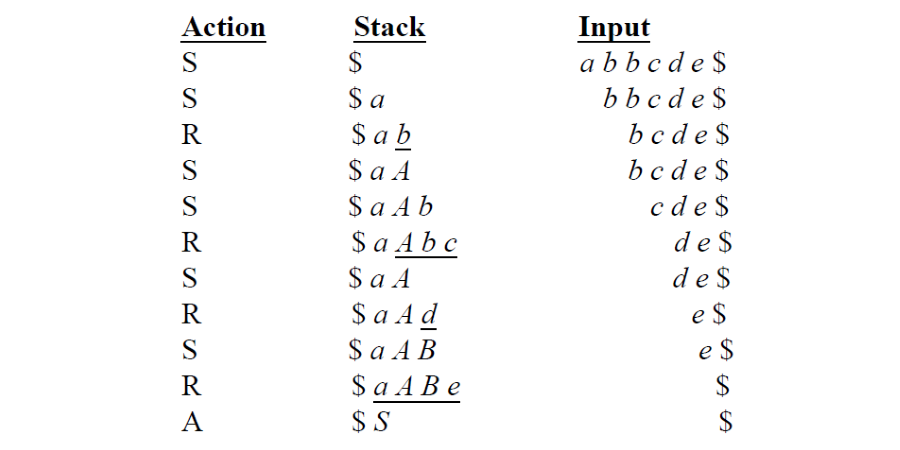
4.6 LR(k) Parsing

4.6.2 Items and the LR(0) Automaton
4.6.4 SLR Parsing

目前流行的 Bottom-UP Parsing 都基於 LR(k) Parsers 的概念，幾乎可以支援所有 CFG，但是建立 Parser 很麻煩，因此通常會使用 Parser generator 來建立 Parser

LR(k) Parsing:

L 代表從左往右掃描輸入
R 代表以 rightmost derivation 進行推導
k 代表作出語法分析決策時的 Lookahead 輸入字元數

這裡會介紹三種 LR Parsing:

SLR(1) Parsing
LR(1) Parsing
LALR(1) Parsing

從狀態數量來說 SLR > LALR > LR，但是能處理的 Grammar 來說 LR > LALR > SLR

4.6.2 Items and the LR(0) Automaton

An LR(0) itemof a grammar in G is a production of G with a dotat some position of the right-hand side, A -> α⋅β
An LR(0) item represents a statein an NPDA indicating how much of a production we have seen at a given point in the parsing process
- NPDA means Non-deterministic Pushdown Automaton
- DPDA means Deterministic Pushdown Automaton

如果有一個 Production A -> XYZ，那他將會有四個 LR(0) item:

A -> ⋅XYZ, A -> X⋅YZ, A -> XY⋅Z, A -> XYZ⋅

這個點代表 Parse 的進度，藉由這些 item 我們可以建立一個 NPDA，再透過演算法來轉換成 DPDA，這個 DPDA 就是 LR(0) Automaton

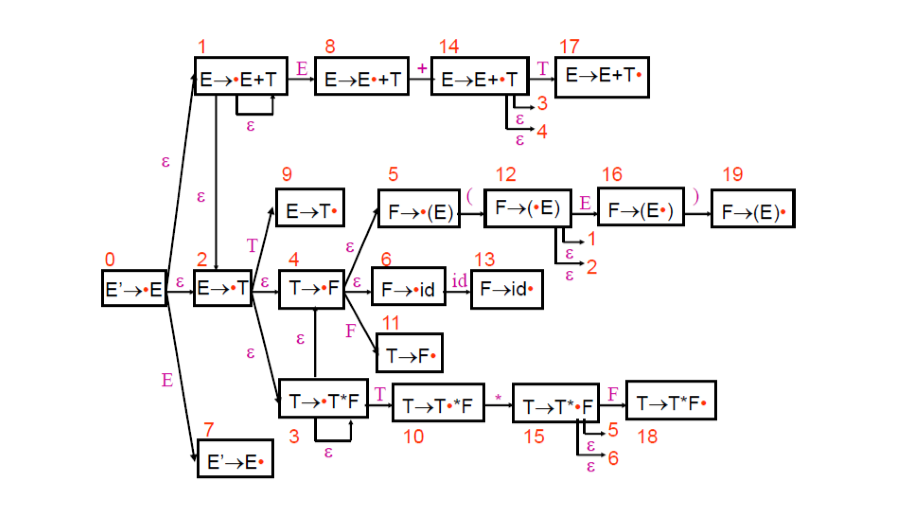
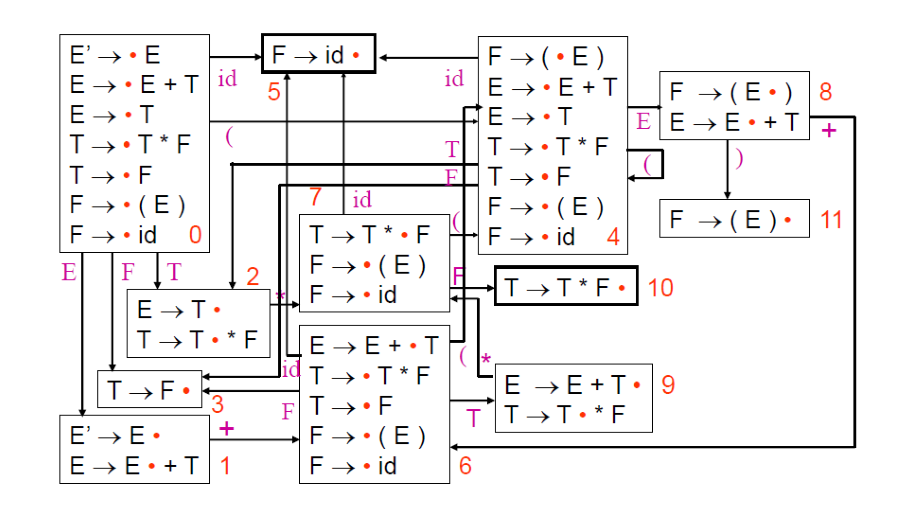
上圖左為 NPDA，右為 DPDA，透過以下演算法將 NPDA 轉換成 DPDA:

functionitems(G');
begin
    C:= {closure({S' -> •S})}
    repeat
        for each set of items I in C and each symbol X do
            J := goto(I, X)
            if J is not empty and not in C then
                C= C ∪ {J}
    until no more sets of items can be added to C
    return C
end

為了建構以上演算法我們需要以下函數與 Augmented grammar(加強語法):

Augmented grammar:
- 加入新的起始符號 S’，並且加入 Production S’ -> S
closure(I) adds more items to Iwhen there is a dot to the left of a nonterminal (corresponding to ε edges)
goto(I, X) moves the dot past the symbol Xin all items in Ithat contain X (corresponding to non-ε edges)

function closure(I);
begin
    J := I;
    repeat
    for each item A -> α•Bβ in J and 
    each production B -> γ in G such that
    B -> •γ is not in J do
        J = J ∪ {B -> •γ}
    until no more items can be added to J;
return J
end

function goto(I, X);
begin
    set J to the empty set
    for any item A -> α•Xβ in I do
        add the item A -> αX•β to J
    return  closure(J)
end

4.6.4 SLR Parsing

以下是 SLR 的演算法

procedure SLR(G');
begin
    for each state Iin items(G') do begin
        if A -> α•aβ is in I and goto(I, a) = J for a terminal a then
            action[I, a] = "shift J"
        if A -> α• in I and A != S' then
            action[I, a] = "reduce A -> α" for all a in FOLLOW(A)
        if S' -> S• in I then
            action[I, $] = "accept"
        if A -> α• Xβ in I and goto(I, X) = J for a nonterminal X then
            goto[I, X] = J
    end
    all other entries in actionand gotoare made error
end

以之前的 Grammar 為例，將其變為 Augmented grammar:

1.  E' -> E
2.  E  -> E + T
3.  E  -> T
4.  T  -> T * F
5.  T  -> F
6.  F  -> (E)
7.  F  -> id

透過演算法來找出所有的 Item:

之後將找到的 Item 填入表中:

s_n: 代表 shift 操作，與前往 State n
r_n: 代表 reduce 操作，並且使用編號 n 的 Production
填表時注意 I_n 中是否有 dot 走到最後，如果有就看是哪一個 Production，並填入 r_n
- 如果 Production 是 S’ -> S，那麼就填入 accept
- 要在什麼欄位填入 r_n，就看 FOLLOW(A) 中有哪些 Terminal，就填入哪些 Terminal

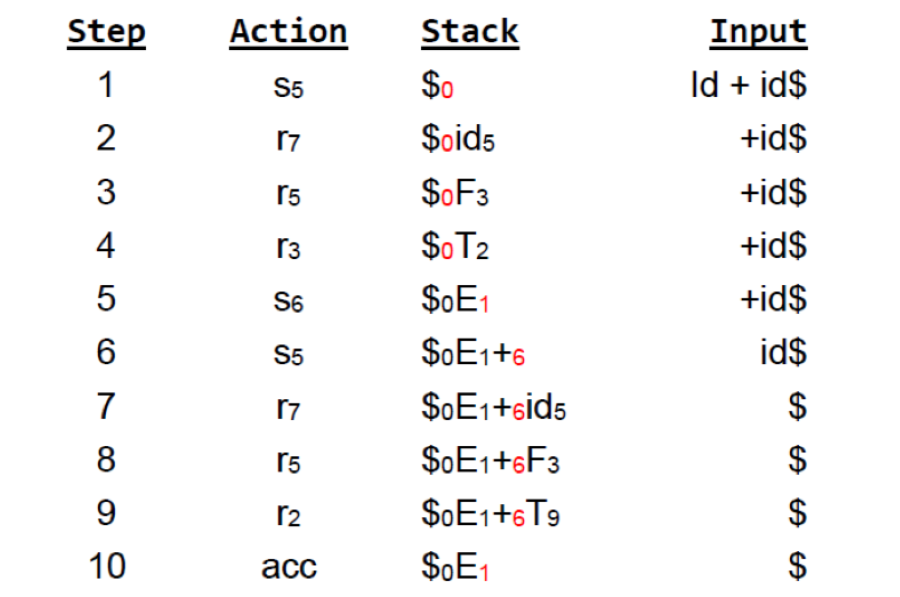
這裡我們用一個測試輸入 id + id 來驗證這個表的正確性，注意做完 reduce 後狀態是看前一個 Stack 中的狀態，再根據 Production 左邊的 Nonterminal 來進行 Goto，所以在 Step 7, 8, 9 是看 State 6 的 goto。

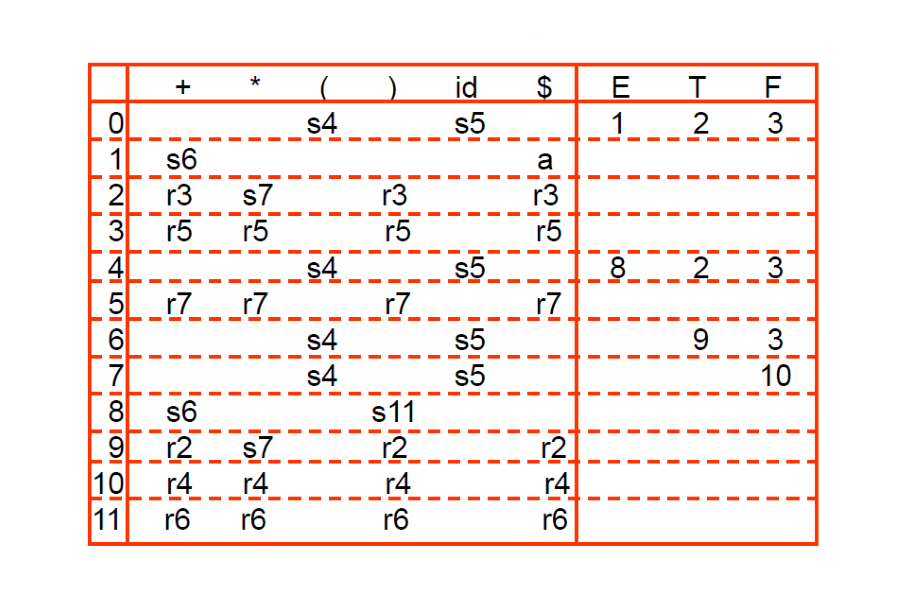
這裡簡單說明上表的範例，以 I2 為例子:

首先注意 E -> T• 代表已經到達 Production 的最後，因此要進行 reduce

FOLLOW(T) = { +, $ ,) }，因此在這三個欄位填入 r₃，3 代表使用第三個 Production

然後這裡還有 E -> E• * T 還沒處理，因此要進行 shift，這裡要看之前的狀態圖把 shift + 放入哪個狀態

這裡是放入 I7，因此 s₇ 在這個例子裡，沒有 Nonterminal 可以被寫入，因此不會填到 goto 欄位

另外說明驗證的過程，直接看到 step 6 7 8 9

Step 6: I6 看到 id，因此 s5 進入 I5

Step 7: I5 看到 $，r7 變成 F，下個狀態要看 I6 的 goto(F) 是 3

Step 8: I3 看到 $，r5 變成 T，下個狀態要看 I6 的 goto(T) 是 9

Step 9: I9 看到 $，r2 變成 E，下個狀態要看 I0 的 goto(E) 是 1
這裡要注意的是做完 reduce 要注意 stack 中還剩下那些狀態，使用那個狀態的 goto

在同一欄遇到多個 reduce 那就需要進行嘗試，直到出現 Error 或是 Accept

4.7 More Powerful LR Parsers

4.7.1 LR(1) Parsing Table
4.7.2 LALR(1) Parsing Table The Core of LR(1) Items

SLR(1) 雖然很簡單，但會有很多 Grammar 不能處理，因此有了更強大的 LR(1) 和 LALR(1)。

LR(1) Parsing: 可以處理最多的 Grammar，但是他的狀態數量也是最多的
LALR(1) Parsing: 可以處理的 Grammar 接近 LR(1)，但是狀態數量基本跟 SLR(1) 一樣

4.7.1 LR(1) Parsing Table LR(1) Items

An LR(1) item of a grammar in G is a pair, (A -> α•β, a), of an LR(0) item A -> α•β and a lookahead symbol a
The lookahead has no effect in an LR(1) item of the form (A -> α•β, a), where β is not ε
An LR(1) item of the form (A -> α•, a) calls for reduction by A -> α only if the next input symbol is a

我們先來看 LR(1) 的演算法:

closure(I) 跟 SLR(1) 不同的是，對於每個 B -> γ，要找出所有可能的 b，b = FIRST(βa)，然後將 (B -> •γ, b) 加入 J 中。 FIRST(βa) 其實就等於先看下一個 Nonterminal 的 FIRST。

function closure(I);
begin
    J := I;
    repeat
    foreach item (A -> α•Bβ, a) in J and 
    each production B -> γ of G that
    each b in FIRST(βa) such that
    (B -> •γ, b) is not in J do
        J := J ∪ {(B -> •γ, b)}
    until no more items can be added to J;
    return J
end

goto(I, X) 其實跟 SLR(1) 一樣，只是 item 多了 lookahead(a)

function goto(I, X);
begin
    set J to the empty set
    for any item (A -> α•Xβ, a) in I do
        add the item (A -> αX•β, a) to J
    return closure(J)
end

下面這是完整的 LR(1) 演算法:

function items(G');
begin
    C := {closure({[S' -> •S, $]})}
    repeat
        for each set of items I in C and each symbol X do
            J := goto(I, X)
            if J is not empty and not in C then
                C := C ∪ {J}
    until no more sets of items can be added to C
    return C
end

整個 Closure 的算法就是:

(A -> α•Bβ, a) 先找出所有的 B -> •γ

計算 b = FIRST(βa)

B 後面的符號加上 a 的 FIRST

之前找出的 B -> •γ 全部都加上 b 作為 lookahead

Example:

 S' -> S
 S  -> CC
 C  -> cC
 C  -> d

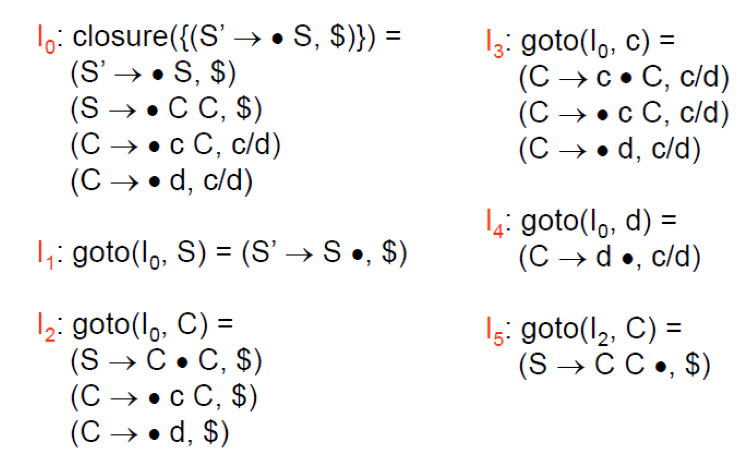
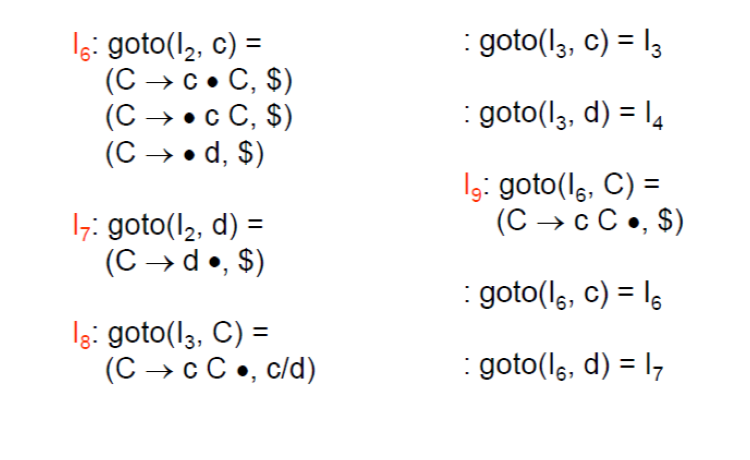
首先看 closure({(S’ -> •S, $)}):
1. 首先計算 (S’ -> •S, $)
  - 以 (A -> α•Bβ, a) 來看會等於 A = S’, α = ε, B = S, β = ε, a = $
  - 加入 B -> •γ，也就是 S -> •CC
  - 計算 b = FIRST(βa) = FIRST(ε$) = { $ }
  - 加入 (S -> •CC, $)
2. 計算 (S -> •CC, $)
  - 以 (A -> α•Bβ, a) 來看會等於 A = S, α = ε, B = C, β = C, a = $
  - 加入 B -> •γ，也就是 C -> •cC, C -> •d
  - 計算 b = FIRST(βa) = FIRST(C$) = { c, d }
  - 加入 (C -> •cC, c), (C -> •cC, d), (C -> •d, c), (C -> •d, d)
  - 簡化為 (C -> •cC, c/d), (C -> •d, c/d)
3. 已經沒有 Item 可以加入，所以返回 I₀
goto(I₀, S): (S’ -> S•, $)
goto(I₀, C):
1. (S -> C•C, $)
  - 以 (A -> α•Bβ, a) 來看會等於 A = S, α = C, B = C, β = ε, a = $
  - 加入 B -> •γ，也就是 C -> •cC, C -> •d
  - 計算 b = FIRST(βa) = FIRST(ε$) = { $ }
  - 加入 (C -> •cC, $), (C -> •d, $)
goto(I₀, c)
1. (C -> c•C, c/d)
  - 以 (A -> α•Bβ, a) 來看會等於 A = C, α = c, B = C, β = ε, a = c/d
  - 加入 B -> •γ，也就是 C -> •cC, C -> •d
  - 計算 b = FIRST(βa) = FIRST(εc/d) = { c/d }
  - 加入 (C -> •cC, c/d), (C -> •d, c/d)

之後就依此類推，直到沒有新的 Item 可以加入，最後就會得到以下的 LR(1) Parsing Table:

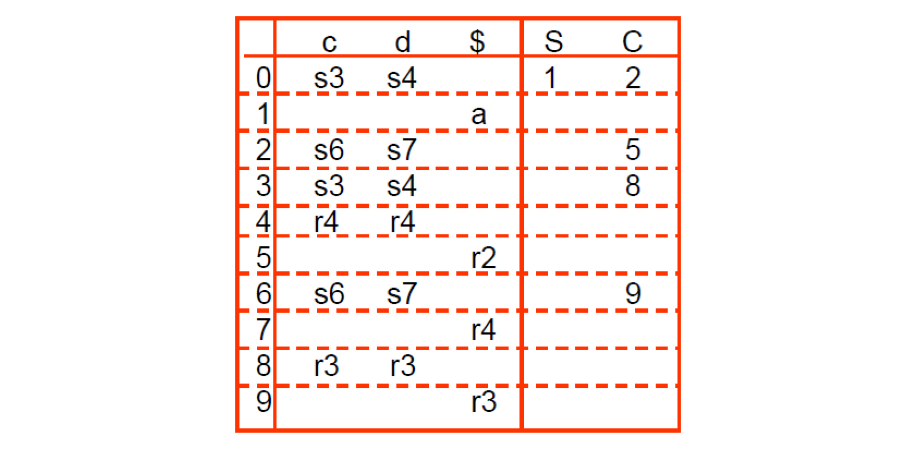
這張表的寫法基本上跟 SLR(1) 一樣，只是 reduce 的部分變成要看 lookahead(a) 是什麼，而不是 FOLLOW(A)

4.7.2 LALR(1) Parsing Table The Core of LR(1) Items

LALR 透過合併 LR 的狀態來減少狀態數量
- 將 LR(1) 中 core 相同的狀態合併

procedure LALR(G');
begin
    for each state I in mergeCore(items(G')) do begin
        if (A -> α•aβ, b) in I and goto(I, a) = J for a terminal a then
            action[I, a] = "shift J"
        if (A -> α•, a) in I and A != S' then
            action[I, a] = "reduce A -> α"
        if (S' -> S•, $) in I then 
            action[I, $] = "accept"
        if (A -> α•Xβ, b) in I and goto(I, X) = J for a nonterminal X then
            goto[I, X] = J
    end
    all other entries in actionand gotoare made error
end

以之前的例子為例，將 Core 相同的狀態合併:

I₃ 和 I₆ 合併就寫作 I₃₆
在合併的同時 Lookahead 也要合併，例如 I₄₇
- I₄ 的 Lookahead 是 c/d，I₇ 的 Lookahead 是 $，合併後 Lookahead 就是 c/d/$

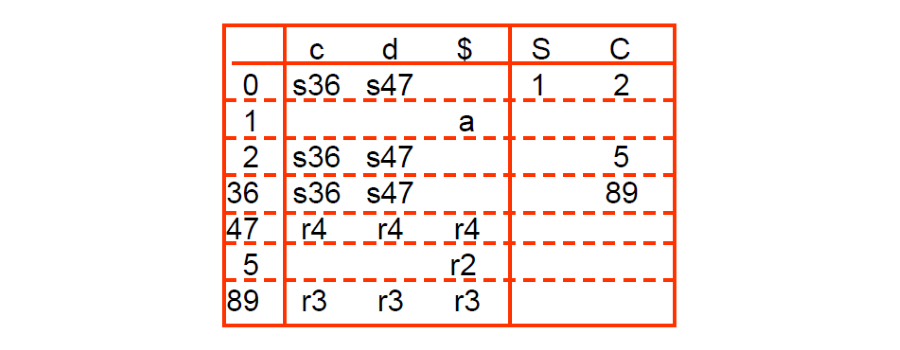
這裡可以發現其實直接從 LR(1) 的表格轉換成 LALR(1) 的表格是很簡單的，找到相同的 core 就可以去按照表格合併

4.8 Using Ambiguous Grammars

要注意所有的 Ambiguous Grammar 都不是 LR(1) 的，LR(1) 的 Parsing Table 不會產生 multiply-defined entries

A grammar is SLR(1) iff its SLR(1) parsing table has no multiply-defined entries
A grammar is LR(1) iff its LR(1) parsing table has no multiply-defined entries
A grammar is LALR(1) iff its LALR(1) parsing table has no multiply-defined entries

一個 Grammar 如果產生 SLR/LR/LALR Parsing Table 並且沒有 multiply-defined entries，那麼就可以稱這個 Grammar 是 SLR/LR/LALR grammar， multiply-defined entries 也可以稱為 conflict(衝突)，例如:

shift-reduce conflict: 一個狀態同時有 shift 和 reduce 的動作
reduce-reduce conflict: 一個狀態同時有兩個 reduce 的動作

一個 grammar 可以是 LALR(1) grammar 但不是 SLR(1) grammar，例如下面的題目:

Exercise 4.7.4:

Show that the following grammar
S -> Aa | bAc | dc | bda
A -> a
is LALR(1) but not SLR(1).

先求出 FLLOW Set:

FLLOW(S) = { $ }
FLLOW(A) = { a, c }

將其轉換成 LR(1) 與 SLR(1) 的 DPDA Graph(Left LR(1); Right SLR(1)):

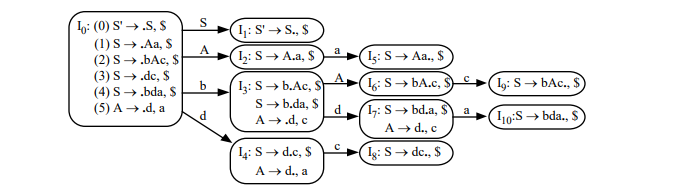
上圖是 LR(1)/LALR(1) 的 Parsing Table 與 Graph，並沒有 conflict 產生

因為沒有可以合併的 core，所以最後 LALR(1) 將會與 LR(1) 相同，並且 LR(1) 並不會產生 multiply-defined entries，所以 LALR(1) 也不會產生 multiply-defined entries，因此這個 Grammar 是 LALR(1)的。

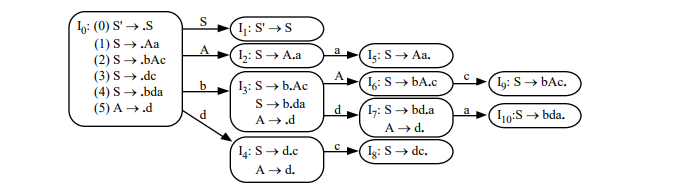
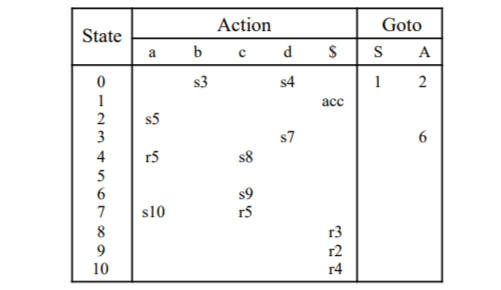
上圖是 SLR(1) 的 Graph

但是我們在 SLR(1) 的 I₇ 可以看到當下一個輸入為 a 時，因為 FLLOW(A) = { a, c }，此時會產生要使用 A -> d 進行 reduce，還是要 shift a 進入 I₁₀ 的 conflict，因為有 conflict 產生，所以這個 Grammar 不是 SLR(1) 的。

4.8.1 Hierarchy of Grammar Classes

如果把 Parsing 能處理的 Grammar 範圍畫成圖就會類似下圖:

如果一個 grammar 以及是 ambiguous 那麼勿論什麼 parsing 都不能處理這個 grammar
Top-Down: LL(k) 相較於 LR(k) 能處理的 grammar 少，但沒辦法和 SLR, LALR 做比較
Bottom-Up: 能處理的 grammar 從多到少依序為，LR(k) > LALR(k) > SLR(1)

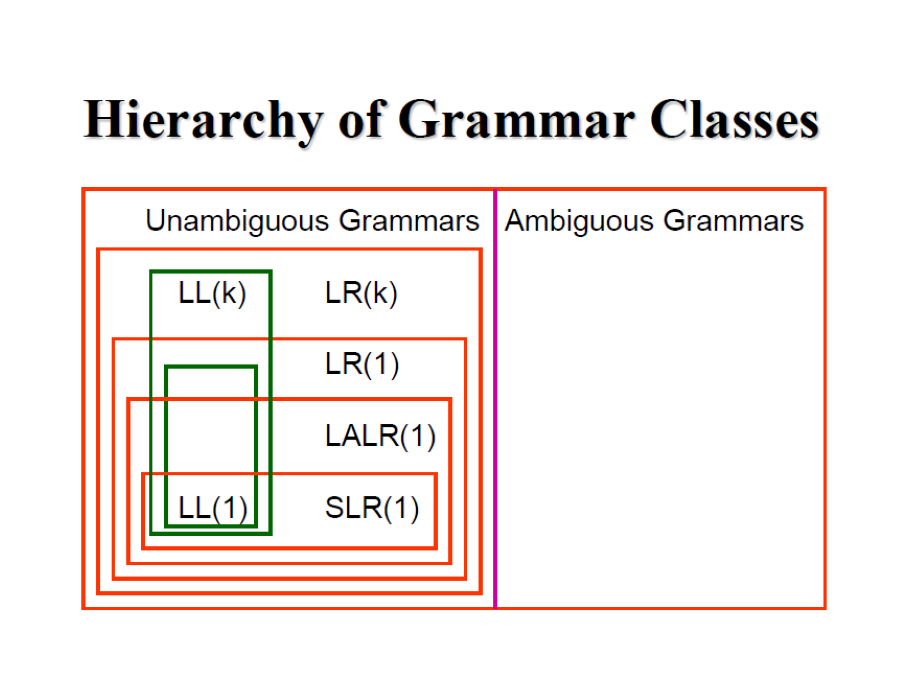
接下來就依序解釋為什麼會有這樣的差異

LL(k) vs. LR(k)

For a grammar to be LL(k), we must be able to recognize the use of a production by seeing only the first k symbols of what its right-hand side derives
For a grammar to be LR(k), we must be able to recognize the use of a production by having seen all of what is derived from its right-hand side with k more symbols of lookahead

簡單的說法就是，LR(k) 是 rightmost 推導，所以結合 lookahead 可以更好的知道該執行 shift/reduce

LALR(k) vs. LR(k)

The merge of the sets of LR(1) items having the same core does not introduce shift/reduce conflicts
Suppose there is a shift-reduce conflict on lookahead a in the merged set because of
1. (A -> α•, a)
2. (B -> β•a γ, b)
Then some set of items has item (A -> α•, a) , and since the cores of all sets merged are the same, it must have an item (B -> β•a γ, b) for some c
But then this set has the same shift/reduce conflict on a

如果一個 LR(1) 沒有 shift/reduce conflict 那麼由合併的 items 也必然沒有 shift/reduce conflict，但如果本來 LR(1) 就有 shift/reduce conflict 那麼合併後會繼承已有 shift/reduce conflict

The merge of the sets of LR(1) items having the same core may introduce reduce/reduce conflicts
As an example, consider the grammar
S’ -> S
S -> a A d | a B e | b A e | b B d
A -> c
B -> c
that generates acd, ace, bce, bcd
The set {(A -> c•, d), (B -> c•, e)} is valid for acx
The set {(A -> c•, e), (B -> c•, d)} is valid for bcx
But the union {(A -> c•, d/e), (B -> c•, d/e)} generates a reduce/reduce conflict

但合併 items 可能會產生 reduce/reduce conflict，因為合併後也會合併 lookahead，這樣有可能使原本沒有 conflict 的 items 產生 conflict，因此產生 reduce/reduce conflict。

SLR(k) vs. LALR(k)

SLR(k) 與 LALR(k) 我們用一個例子來說明:

As an example, consider the grammar
S’ -> S S -> L = R S -> R L -> * R L -> id R -> L

FOLLOW(R) = { =, $ }

先看 SLR(1) 的 Items set，因為是使用 FOLLOW(R) 來進行 reduce，所以在 I₂ 產生 shift/reduce conflict，在 I₂ 可以 shift =，也可以使用 R -> L 進行 reduce，因為 FOLLOW(R) = { =, $ }。

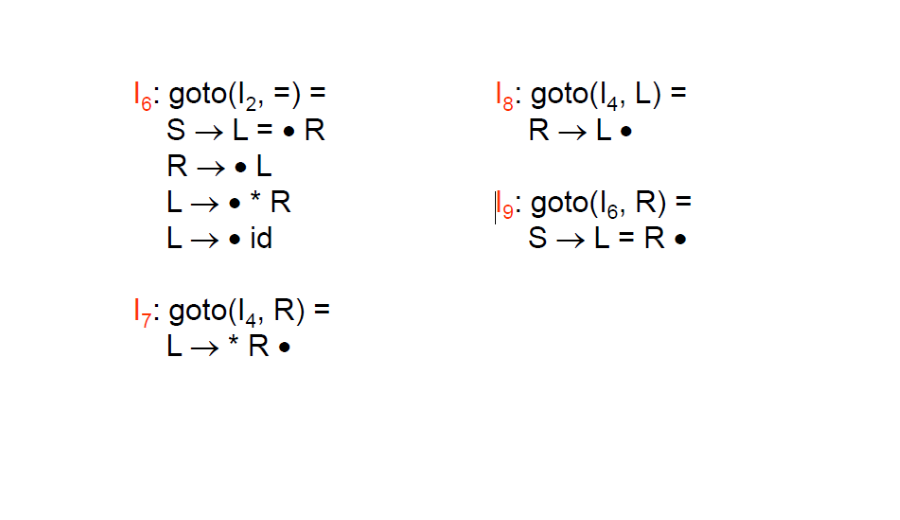
在 LALR(1) 因為從 LR(1) 合併而來，因此有 lookahead 的存在，所以即使在 core 相同的時候，也可以透過 lookahead 來區分是否要進行 reduce。

Last Edit 11-27-2023 16:19

還有一個部分是使用 bison 來實作 Syntax analysis，但這個篇章已經很長了，所以我會放在另一篇講述如何實作

results matching ""

No results matching ""

, Compiler