Note | Constraint Satisfaction Problem

Introduction to Artificial Intelligence Week 6 Notes

CSPs Introduction

Constraint Satisfaction Problem 其定義為一組物件，而這些物件需要滿足一定的限制或條件，而這個問題可能有很多的解。CSP 問題經常表現出高複雜性，需要結合啟發式搜尋和搜尋方法來在一個合理的時間內解決問題。

主要解法：通過識別違反約束的變量與值的組合消除大規模的搜索空間。

• CSP related
  • Linear programming
  • Nonlinear progaramming
  • Numerical analysis
• CSP application
  • Operations research
  • Network flows
  • optimization problems

CSP Define

定義一個 3-tuple(X, D, C) 其中
X = {X1, …, Xn} Finite set of variables.
D = {D1, …, Dn} Nonempty domain of possible values for each variable.
C = {C1, …, Cn} Finite set of constraints, Each constraint Ci limits the values that variables can take.

Example

Map coloring 就是一個經典的 CSP。每個區域即是變數，顏色便是值域，相鄰區域顏色不同是約束。

其中關於 Constraint 可被劃分為:

• unary constraint: 只約束單個 variable 的取值。如 SA 不能被染成綠色。
• binary constraint: 兩個 variable 相關的約束。如 SA 不能與 WA 的顏色相同。
• global constraint: 全局約束。如 Alldiff, 即約束中所有 variable 皆需取不同的值。

Arc Consistency example

Backtracking search for CSPs

回朔搜索，用於 DFS 中。他每次為 Single variable 進行取值，當沒有合法的值可給某個 variable 時就進行回朔。

• 為使 search 變的高效，須解決以下問題:
  1. 下一步應該給哪個 variable 取值? 按照什麼順序取值?
  2. 每步 search 應該做怎樣的推理?

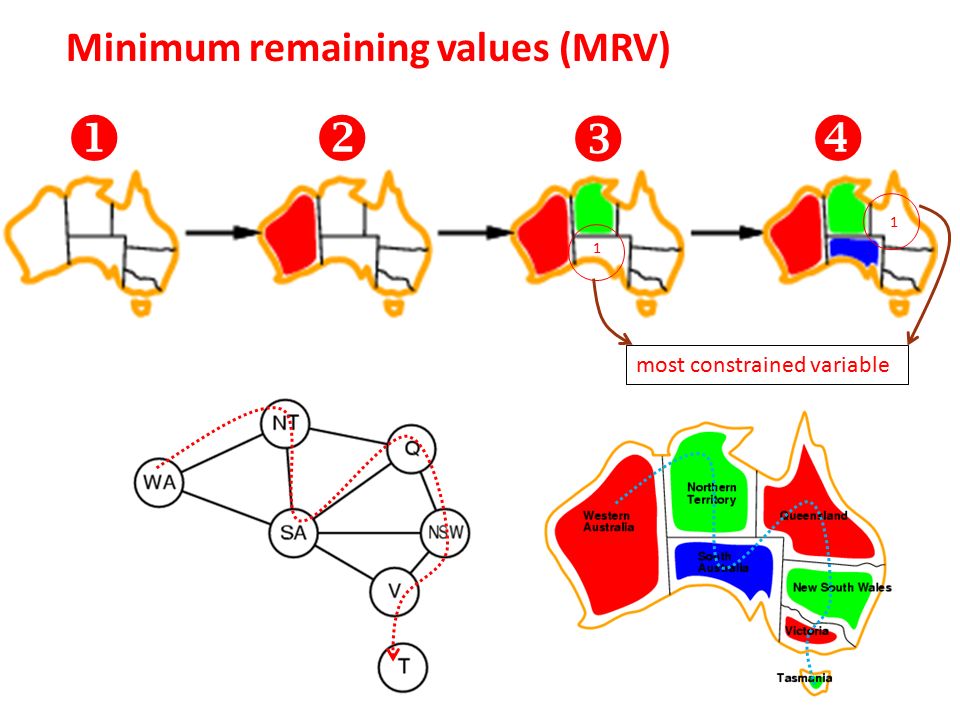
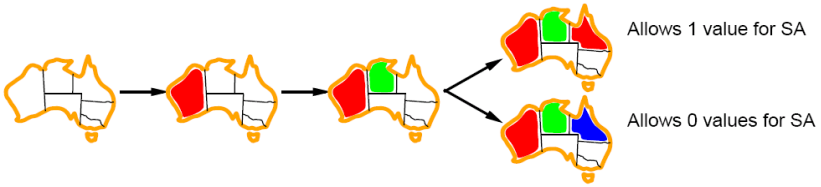
Variable select: Minimum remaining values (MRV)

最少剩餘值啟發式: 選擇合法取值最少的 variable 開始。這樣選擇的 variable 可能很快地導致失敗，從而進行回朔。

Degree heuristic

鄰接度啟發式: 選擇與其他未取值 variable 約束最多的 variable 來試圖降低未來可能的分支。

Value order

Least constraining value (最少限制值): 選擇 value 時優先選擇給鄰居 variable 留下最多選擇的分支。

Inference in CSPs

在 CSP 問題中，Algorithm 可以進行搜索，也可以做約束傳播 (The constraint propagation) 的推理

約束傳播: 使用約束來減少一個 variable 的合法取值範圍，從而影響與此 variable 有約束關係的另一個 variable 的取值。 (局部相容性)

Node Consistency (節點相容)

Single variable (In CSP Single node) 值域中的所有取值滿足他的 unary constraint.

if SA = NA = {Red, Blue, Green};
SA != Blue, NA != Red, SA = {Green, Red}, NA = {Blue, Green};

Arc Consistency (弧相容)

CSP 中某 variable range 所有取值滿足該 variable 的所有 binary constraint.

最常用的算法為 AC-3, 算法流程大致如下:

1. Get all the constraint and turn each one into two arcs.
   Expmale: A > B becomes A > B and B < A.
2. Add all the arcs to a queue.
3. Repeat until the queue is empty:
   3.1. Take the first arc (𝑥, 𝑦), off the queue (dequeue).
   3.2. For every value in the 𝑥 domain, there must be some value of the 𝑦 domain.
   3.3. Make 𝑥 arc consistent with 𝑦. To do so, remove values from 𝑥 domain for which there is no possible corresponding value for 𝑦 domain.
   3.4. If the 𝑥 domain has changed, add all arcs of the form (𝑘, 𝑥) to the queue (enqueue). Here 𝑘 is another variable different from 𝑦 that has a relation to 𝑥.

Forward Checking

向前檢驗是最簡單的推理形式，只要 X variable 被賦值了，就向前檢驗過程對他做 Arc Consistency. 檢查對於每個通過約束與 X 相關的, 未賦予值的 Y variable, 從 Y 的 range 中消去與 X 不相容的值。

NOTE

待更新