Compiler | Semantic Analysis Notes
Compilers course notes from CCU, lecturer Nai-Wei Lin.
Semantic Analysis 這個階段主要用來檢查程式碼的語意是否正確,如果語意有錯誤則會產生錯誤訊息。
Outline
- Semantic Analyzer
- Attribute Grammars
- Syntax Directed Translation
- Type Checking
- Syntax Tree Construction
- Bottom Up Translators
- Bison A Bottom Up Translator Generator
Semantic Analyzer
狹義上的 Semantic Analyzer(語意分析)只負責 Type checking, 但廣義上的語意分析則可以同時在 Type checking 時進行程式碼的 Interpretation 或 Translation。
- Type checking of each construct
- Interpreation of each construct
- Translation of each construct
5.1 Attribute Grammars
Attribute Grammar(屬性語法) 也可以稱為 Syntax Directed Definition(SDD, 語法導向定義):
- Attribute Grammars 是帶有 Associated semantic attributes(關聯語意屬性)與 Semantic rules(語意規則)的 Context-free grammar
- 每個 Grammar symbol 都關聯一組 Semantic attributes
- 每個 Production 與關聯一組計算屬性的 Semantic rules
Example 5.1 An Attribute Grammar
L -> E '\n' {print(E.val)}
E -> E '+' T {E.val = E.val + T.val}
E -> T {E.val = T.val}
T -> T '*' F {T.val = T.val * F.val}
T -> F {T.val = F.val}
F -> '(' E ')' {F.val = E.val}
F -> digit {F.val = digit.val}
# val represents the value of an expression
例如 E -> E '+' T,他的 Semantic rules 為 E.val = E.val + T.val,其中 E.val 與 T.val 為 Semantic attributes。
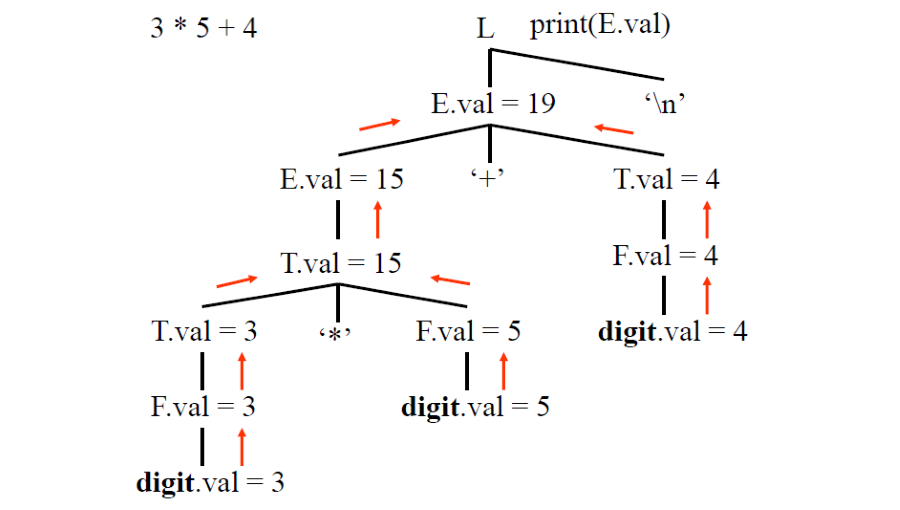
把 3 * 5 + 4 當作範例化成 Syntax Tree 將會如上圖所示
- Synthesized attributes(合成屬性):
如果一個 Node(Grammar symbol) 在解析樹中的屬性值是由其子節點的屬性值計算出來的,則稱該屬性為合成屬性 - Inherited attributes(繼承屬性): 如果一個 Node(Grammar symbol) 在解析樹中的屬性值是由其父節點的屬性值計算出來的,則稱該屬性為繼承屬性
5.1 的例子中可以看出全部都是 Synthesized attributes,下面是 Inherited attributes 的例子
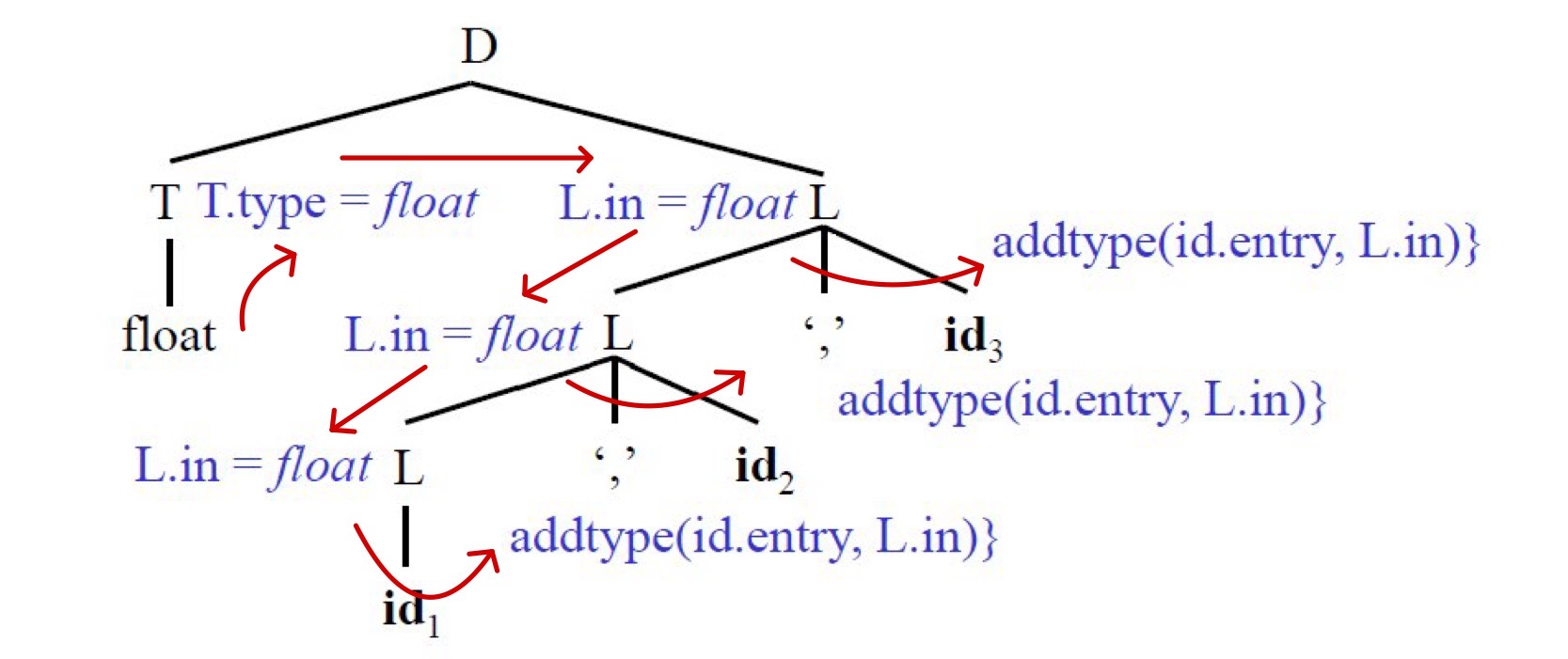
D -> T { L.in := T.type } L
L -> int { L.type := integer }
L -> float { L.type := float }
L -> { L1.in := L.in} L1 ',' id { addtype(id.entry, L1.in) }
L -> { addtype(id.entry, L.in) }
S-Attributed Attribute Grammar
- 如果一個 Attribute Grammar 的每個 Attribute 都是 Synthesized attributes,則稱為 S-Attributed Attribute Grammar
L-Attributed Attribute Grammar
- An attribute grammar is L attributed if each attribute in each semantic rule for each production
A -> X1 X2 … Xn is a synthesized attribute, or an inherited attribute of Xj , 1 <= j <= n, depending only on- the attributes of X1 , X2 , …, Xj-1
- the inherited attributes of A
簡單來說就是如果一個 attribute 所使用的「資訊來自上層或左邊」,則稱為 L-Attributed Attribute Grammar
A Counter Example
這裡簡單舉一個錯誤的例子:
A -> { L.in := l(A.in) } L { M.in := m(L.s) } M { A.s := f(M.s) }
A -> { Q.in := q(R.s) } Q { R.in := r(A.in) } R { A.s := f(Q.s) }
在這裡使用到了 R.s 因此導致錯誤,要注意 R.s 應該是來自於 R,但是在這裡 R 還沒有被計算出來。
Attribute Parse Tree
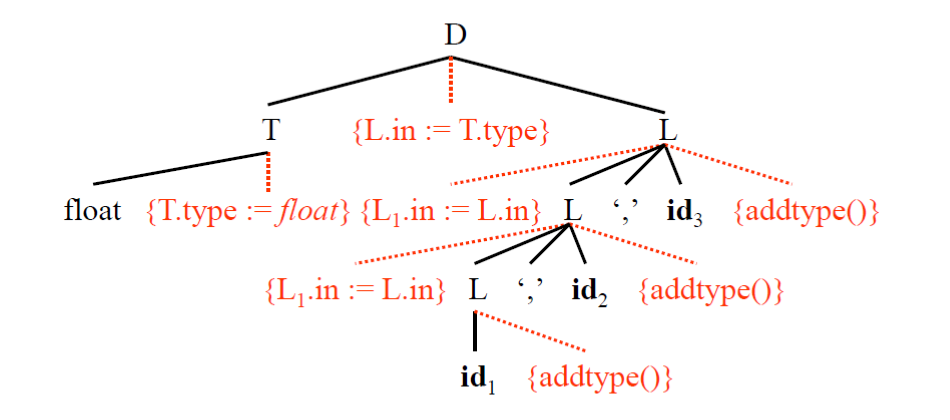
這裡表示一種名為 Attribute Parse Tree(屬性解析樹)的資料結構,虛線的位置表示語意規則,實線的位置解析的語法規則。 這樣整棵樹就能以一種 Preorder 的方式來計算出所有的 Semantic attributes。
Example
E -> T { R.i := T.s } R { E.s := R.s }
T -> num { T.s := num.val }
R -> addop T { R1.i := R.i addop.lexeme T.s } R1 { R.s := R1.s }
R -> ε { R.s := R.i }
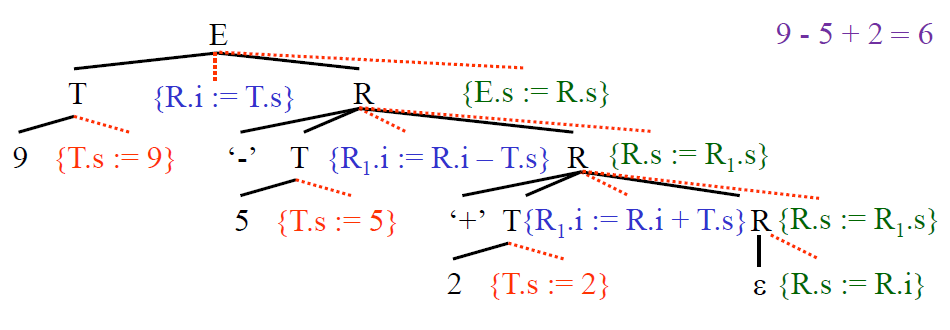
上面是一個直譯的例子,最後在 Root 能求出 E.s 的值
Type Checking
在這裡所談的是 Static Type Checking(靜態型別檢查),也就是在編譯時期就能檢查出來的型別錯誤。
這邊可以把 Type 的應用分為兩種:
- Type Checking(型別檢查)
- 型別檢查確保運算子(Operator)與運算元(Operand)的型別是相容的,例如: Java 規定 && 的兩邊必須是 boolean
- Translation application
- 根據型別的名稱,Compiler 可以決定需要多大的記憶體空間,這些資訊還會被很多後續的階段使用,例如: Array 中的起始位置,進行運算時的型別轉換等等…
5.2 Type Systems
- Type system(型別系統)是一種用來描述程式語言中的型別的規則,而 Type checker(型別檢查器)實現了這些規則
- Type expression(型別表示式)是一種用來描述型別的方式,例如:
int x,宣告了一個名為 x 的變數,型別為 int
Type Expression
- 基本型別
- boolean, int, float, char, real, void, type_error
- 類型構造函數也是一種 Type expression
- array: array(S, T), means an array of T type with size S
- product: T1 x T2 x … x Tn, means a product of T1, T2, …, Tn
- pointer: pointer(T), means a pointer to T type
- function: int function(int, float), means a function that takes an int and a float and returns an int.
Type Checker
- 通過宣告的時候把型別資訊與對應的 Identifier 放入符號表(Symbol Table)
- 這樣在表達式中就能透過符號表來檢查 Identifier 的型別是否正確
Type Checking of Expressions
這裡展示一個可能的型別檢查的規則:
E -> literal { E.type := char }
E -> num { E.type := int }
E -> id { E.type := lookup(id.name).type }
E -> E1 mod E2 { if E1.type == int and E2.type == int then E.type := int else E.type := type_error }
在 mod 的語意規則中,加入了型別檢查的規則,如果 E1 與 E2 的型別都是 int,則 E 的型別也是 int,否則 E 的型別為 type_error, 這樣在後續的處理就能夠判斷出來是否有錯誤。
Postfix Translation Scheme
Postfix Translation Scheme(後序翻譯方案)是一種用來描述語法規則的方式,假如一個文法是 S-Attributed Attribute Grammar, 那在 LR 中就能夠使用 Postfix Translation Scheme 來描述語法規則。
5.3 Bottom-Up Translators
因為在 Bottom-Up 的過程中我們會有一個 Stack 紀錄已經解析過的 Token,因此我們也可以透過這個 Stack 來傳遞 Attribute。

- 假如有一個語法規則 A -> XYZ, { A.a := f(X.x, Y.y, Z.z) }
- 如果要對這個語法規則做 Reduce,那麼 Stack 中必然已經存在依序的 XYZ
- 此時就可以透過偏移量來取得 XYZ 的 Attribute,例如: val[Top-2] is X.x
- 如果要做 Reduce,最後 A 會存在於消除 XYZ 後的 Stack 最上面,因此會與 X 的位置相同,也就是 val[Top-2]
Example
這裡給出一個例子,實際上在 Bison 中使用時會有一些差異,但是大致上是相同的。

下圖是以這個例子來建立的例子
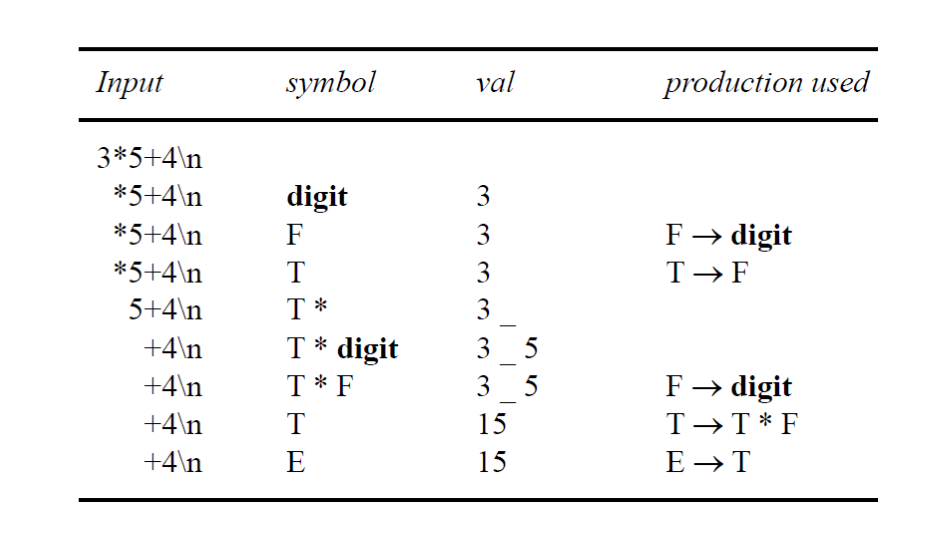
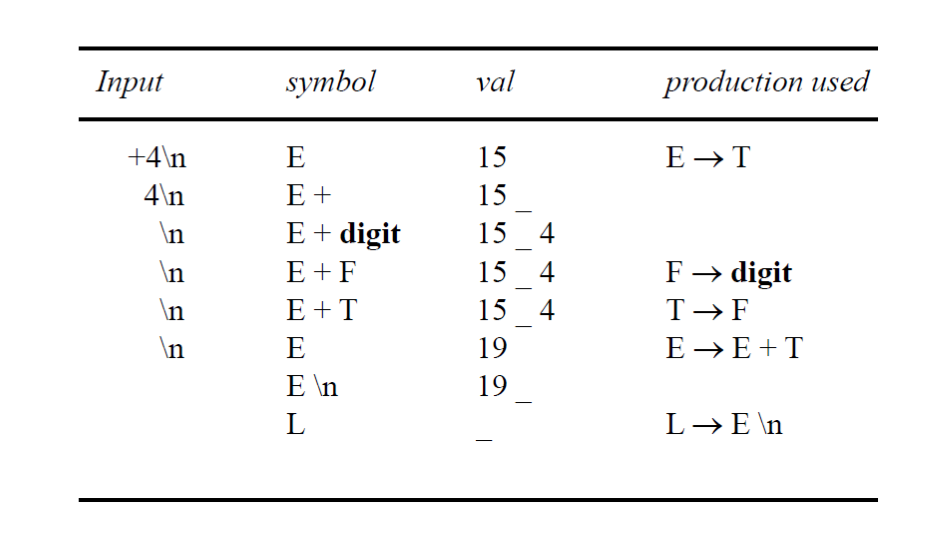
實際上這樣的方法並不好用,因為在 Bison 中如果想要手動處理 Stack 的偏移,尤其是 -1 這種偏移量,會非常的麻煩
延伸閱讀: Bison 3.4.6 Actions, 這裡會提到如何使用 $0, $-1 等方式來取得 Stack 中的值
參考範例: negative_stack.y 這裡是可以參考的範例
Syntax Tree Construction
5.3 Syntax Tree Construction
在這裡我們能發現在 Syntax Analysis 的時候,Bottom-up 的 Parser 是比較強大的方法,因為能透過 lookahead 等方法提前知道後續的 Token, 但是在 Semantic Analysis 的時候,Top-down 的 Parser 是比較強大的方法,因為在傳遞 Attribute 的時候,Top-down 的 Parser 能夠很容易的傳遞 Attribute。
而這裡會使用一種 Abstract Syntax Tree(抽象語法樹)來表示語法結構,這是一種 IR(Intermediate Representation, 中間表示法), 透過這個資料結構我們就能排除掉 Bottom-up 或 Top-down 的 Parser 的難點。
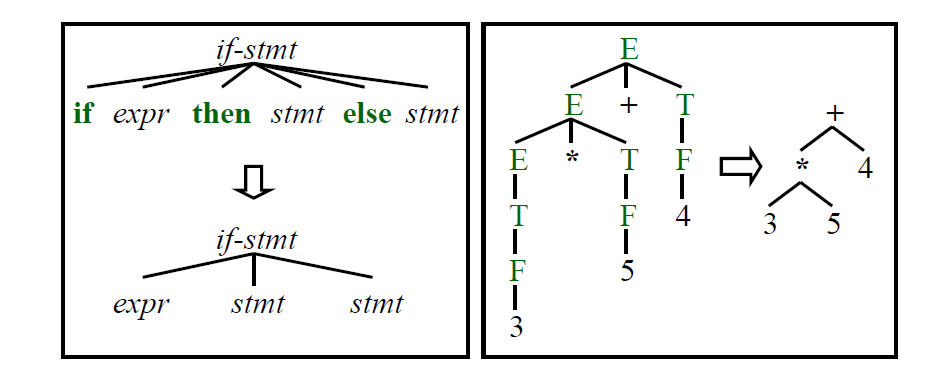
Syntax Tree for Expression
- Interior nodes(內部節點)表示運算子,例如:
+, -, *, /, mod - Leaf nodes(葉節點)表示運算元,例如:
literal, identifier, num - 假設建構節點的函數如下:
- mknode(op, left, right)
- mkleaf(id, entry)
- mkleaf(num, value)
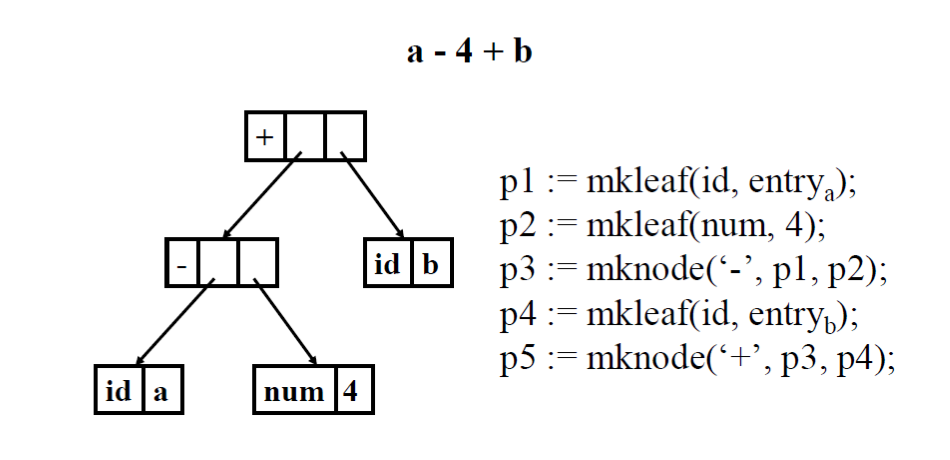
上圖展示了一個 a - 4 + b 的 AST
Last Edit
11-29-2023 18:10